Retranscription des épisodes 237 et 239 de Podcast Science :

Nous avons reçu, pour la dernière émission de la saison 5, Jean-Philippe Uzan, qui nous a avoué son amour pour le mot cosmos, signifiant en grec a la fois la beauté et l’univers. Dans la foulée, il nous a donné plusieurs mots en découlant, de la cosmologie (science de l’univers tout entier), à la cosmogonie (théories de l’origine de l’univers). Il a aussi parlé de cosmothanatologie, mot nettement moins utilisé et désignant les théories de mort de l’univers. Je voudrais cette semaine vous parler de cosmographie, du grec cosmos et graphein, qui veut dire écrire. De la même façon que la géographie (du grec gaia, la Terre et graphein écrire), la cosmographie est la science très ancienne de la description de l’univers dans son ensemble. À quoi ressemble la carte de l’univers ? Et la question qui vient tout de suite après est : “où se trouve le point rouge : Vous êtes ici ? ”. En clair, où sommes nous ?

D’où viens-je ? Où cours-je ? Dans quel état j’erre ?

Ceux qui ont vu le spectacle d’Alexandre Astier, l’Exoconférence savent que plusieurs civilisations humaines ont tenté de donner une organisation à l’univers de manière plus ou moins imagée. La cosmographie nordique imagine ainsi un immense Arbre du Monde nommé Yggdrasil comportant 9 mondes différents, dont les plus célèbres sont l’Asgard, situés dans le ciel et monde des dieux associés à Odin,  le Midgard, monde des hommes situés au niveau de la terre et le Helheim, qui est le monde des morts, sous la Terre et qui a donné en anglais hell, l’enfer. Il est assez intéressant de noter que contrairement à la mythologie chrétienne, il existe d’autres mondes au dessus du monde des dieux d’Asgard et un autres mondes en dessous du monde des morts, ce qui selon moi est la meilleur façon de motiver les évolutions de carrière pour tous. Midgard, le mondes des hommes est quant à lui entouré par le monde du gel au nord et le monde du feu au sud et est entouré entièrement par l’immense serpent Jörmungand qui se mord la queue. S’inspirant de mythologies indiennes existant réellement, l’auteur de fantaisie Terry Prachett imagine quant à lui une cosmographie où un monde disque serait posé sur 4 éléphants, eux mêmes supportés par une grande tortue cosmique.

On peut se moquer mais jusqu’à la renaissance en Europe, on utilise la cosmographie de Ptolémée qui stipule que la Terre est ronde et située au centre de l’univers. Autour d’elle se trouve des sphères de cristal (ce qui explique que l’on ne les voit pas) sur lesquelles sont attachées la lune, le soleil, les planètes connues (Mercure, Venus, Mars, Jupiter, Saturne) et une ultime sphère, limite de l’univers, sur laquelle sont attachées toutes les étoiles. Je vais passer rapidement sur la révolution copernicienne (Jean-Pierre Luminet, que nous avions reçu à l’épisode 211 la décrit très bien dans une une courte vidéo). La plupart de nos auditeurs savent bien de quoi il s’agit et que cette révolution a amené : la terre, au lieu d’être fixe au centre de l’univers tourne maintenant sur elle même et autour du Soleil. Mais si on y réfléchit 5 minutes, c’est très vertigineux : d’un coup, tout se met à tourner dans tous les sens, tous les astres bougent les uns par rapport aux autres, à des vitesses… et bien astronomiques. Et c’est la deuxième question à laquelle je vais tenter de répondre dans ce dossier. Dans quelle direction allons nous ? Et à quelle vitesse ?

Voilà pour l’introduction, on va maintenant partir pour un voyage où chaque étape n’est qu’un microscopique grain de sable projeté à des vitesses incroyables par rapport à l’étape qui vient juste après.

Vitesses dans le système solaire

La Terre fait une rotation sur elle même en une journée environ. Du coup votre vitesse autour du centre de la Terre dépend de l’endroit où vous vous trouver sur le globe. Si vous vous trouvez à l’équateur, un tour correspond à 40’000 km en 24h, ce qui fait donc 1700 km/h environ autour de l’axe Pole Nord Pole Sud (ou 0.5 km/s). Si vous êtes en France, à une latitude de 47 degrés Nord environ, un tour correspond à 20’000 km en 24h, ce qui fait donc 1100 km/h (ou 0.3 km/s) environ autour du centre de la Terre.

Bon, c’est très bien 1700 km/h, mais ça ne vous dit pas grand chose si on ne compare pas un peu à des choses connues. Ce qui est le premier réflexe du physicien, de comparer ses chiffres à ceux qu’ils connait déjà. Si vous nous écoutez et que vous êtes dans un avion de ligne, vous allez environ à 900 km/h (0.25 km/s) par rapport à la surface de la Terre pour les plus rapides. Si vous nous écoutez et que vous êtes dans un avion de chasse, déjà, c’est flatteur, mais s’il vous plait arrêtez de m’écouter en conduisant un avion de chasse. Bon mais vous êtes à 2,450 km/h (0.7 km/s). Oui, alors après il faut additionner ces vitesses, en fonction de si vous allez dans le sens opposé à la rotation de la Terre (si je viens vous voir à Paris depuis la cote Est des États Unis), ou si je vais dans le même sens que la Terre (si je retourne aux états unis en survolant le pacifique). Pourquoi c’est important de donner ces deux vitesses ? Parce que seule l’une d’entre elle est supérieure à la rotation de la Terre et que du coup dans un avion de ligne à des latitudes pas trop importantes, il est normalement impossible d’arriver “avant d’être parti”. Par contre, c’est fréquent avec des avions plus rapides. Si vous êtes sur la station spatiale internationale, c’est vraiment super flatteur et vous pour le coup, vous êtes à 28 000 km/h (7.7 m/s), donc vraiment beaucoup plus vite. Et vous êtes sans doute les humains qui vont le plus vite autour de l’axe Pole Nord Pole Sud.

Bon maintenant, vous tournez à 1100 km/h (ou 0.3 km/s) en France, mais à cela vous ajouter un mouvement de rotation autour du soleil. Ce mouvement est de 107’000 km/h, soit environ 30 km/s. La rotation autour du soleil et celle autour de nous même ne sont pas exactement dans le même plan, il y a un angle de 23 degrés entre les deux (c’est cet angle qui explique en grande partie les saisons par ailleurs). Donc voila, on tourne à 1700 km/h (ou 0.5 km/s) autour du centre de la terre dans un mouvement circulaire, et le tout va à une vitesse de 30 km/s autour du soleil.

Vous vous demandez pourquoi on ne sent pas ces vitesses. En fait il y a deux réponses à ça c’est que l’on ne sent que les accélérations, pas les vitesses. Donc le mouvement circulaire autour du Soleil, on ne le sent pas. Par contre la rotation autour de la Terre, on la sent car on ne fait plus un mouvement de circulaire uniforme, mais un mouvement de rotation. Et donc plus on tourne vite, plus on le sent. Et c’est pour ça qu’il est plus facile de lancer les fusées à de basses latitude et que les européens lancent depuis Kourou, en Guyane, que les américains lancent depuis Cap Canaveral en Floride et que les russes ne lancent même plus depuis la Russie, mais depuis Baïkonour au sud du Kazakhstan. C’est vraiment faible, de l’ordre de 0.5 % plus fort aux pôles qu’à l’équateur, donc nous on le sent pas. Mais les vitesses dans la direction parallèle a la surface sont a accélérations nulle. Et du coup on ne sent rien ! Par contre, si elle s’arrêtait de tourner, là ça serait terrible. Il y a un what if qui parle de la question.

Unité Astronomique

On voit là qu’on commence déjà à saturer nos pauvres unités, bien adaptées pour les déplacement terrestres mais un peu limitées dès qu’on s’en échappe. Si on ne fait pas attention, on va rapidement se retrouver à parler comme quand les journaux grands publics essayent de parler d’astronomie, à parler de 14 millions de millions de milliard de km. Et comme personne ne sait ce que c’est que 14 millions de millions de milliard de km, on comprend plus rien. Vu que je vous fait confiance, je vous vais vous donner les deux trucs des astronomes : premièrement, au bout d’un moment, on ne donne que les premiers chiffre et le nombre de zéro. Ce qui fait que 14 millions de millions de milliards, c’est 14 et 21 zéros derrière, que l’on note 14 x 10²¹. Le deuxième truc auquel je vais tenter de vous initier ce soir, c’est qu’assez rapidement, on ne compte pas en km. C’est exactement comme si, selon que vous vouliez donner rendez vous à quelqu’un dans 30, 300 ou 30 millions de secondes, vous allez choisir une unité adaptée au besoin (secondes, heure, année). Je vais donc tout au long du dossier essayer de vous introduire les unités que les astronomes utilisent pour se simplifier la vie. Par comparaison, je vais essayer parfois de revenir aux unités “terrestres” pour que l’on se fasse une idée.

D’autre part, on voit bien que puisque tout bouge les un par rapport aux autres, on a bien du mal à trouver un point de référence pour donner la vitesse. Pour la première étape, j’ai utilisé un référentiel géocentrique, c’est à dire centré sur le centre de la Terre et j’ai donné notre vitesse par rapport au centre de la Terre, mais pour la seconde, j’ai utilisé un repère héliocentrique, c’est à dire centré sur le centre du Soleil. Pour donner une vitesse, il faudra bien donner un référentiel à chaque étape, et malheureusement, ce ne sera jamais le même, car on a perdu le centre de l’univers avec Galilée et on est pas près de le récupérer.

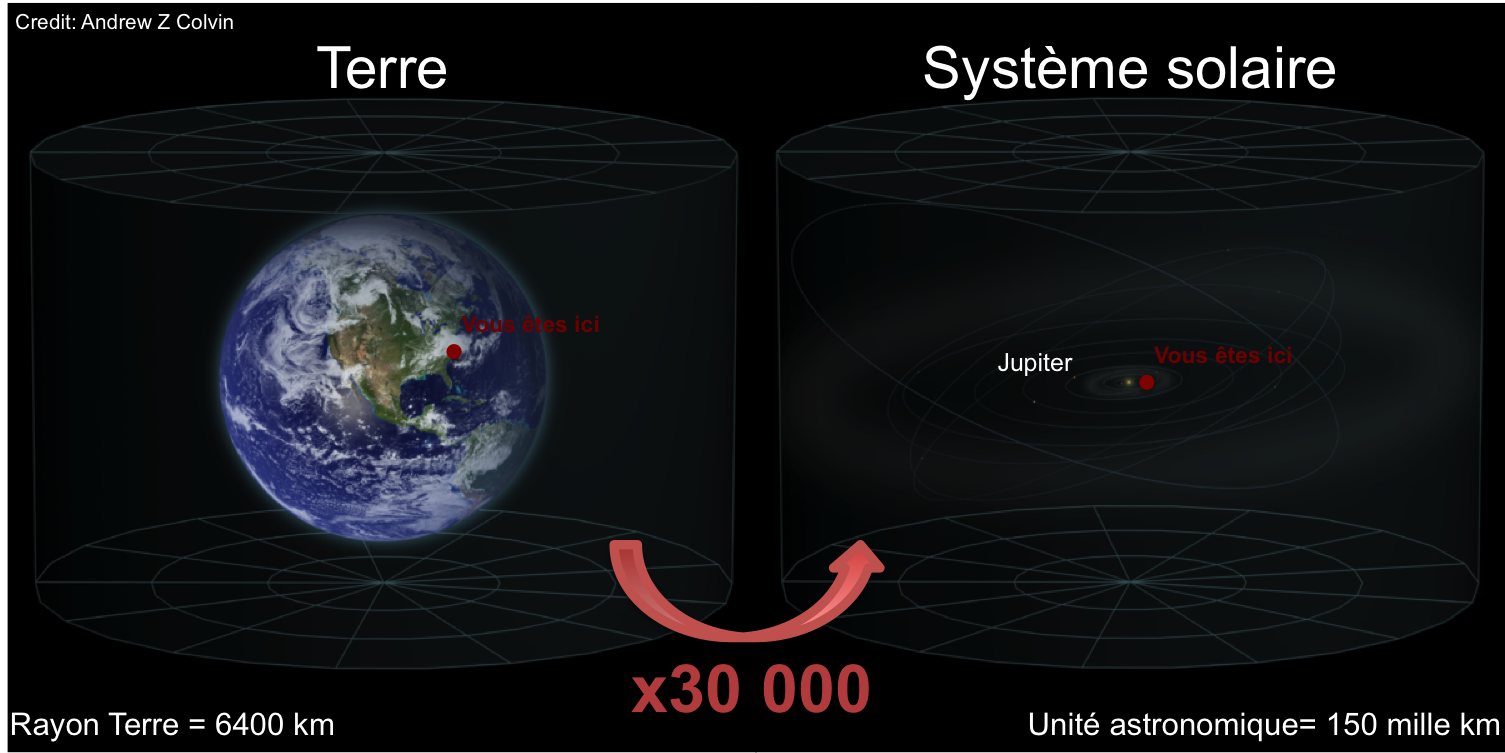
La première unité que j’introduis ici est donc l’unité astronomique (UA en français, AU en anglais). En bons anthropocentristes que nous sommes, cette unité définie la distance entre la Terre, notre planète, et le Soleil, notre étoile, 1,5 x 10¹¹ m (150 millions de km). Elle est donc l’unité parfaite pour les gens qui regardent des distances dans le système solaire ou dans les systèmes stellaires. Moi je compte tous les jours en UA dans mon travail, jamais en km. Voila, on en est rendu là après Copernic et Newton, mais là on est un peu coincé. En effet, les mouvements et les vitesses dans le système solaire, circulaires et répétitifs, peuvent se déduire par l’application des lois de Kepler, généralisées par Newton. Mais il est relativement facile de donner à une vitesse à un objet qui bouge dans le ciel. Mais pour aller plus loin, il faut savoir à quel distance se trouvent et à quel vitesse vont les étoiles autour de nous. Et là on est emmerdés, car ce sont de en apparence des points (on ne peut pas leur donner un rayon, ce sont des points) immobiles dans le ciel d’une nuit à l’autre. Est ce qu’ils sont vraiment immobiles, ou est ce qu’ils bougent à toute vitesse mais sont tellement loin qu’on ne peut pas les voir bouger. On va utiliser une méthode pour donner une distance à ces points, la parallaxe. La parallaxe, c’est la méthode que notre cerveau utilise pour donner une distance aux objets autour de nous.

La parallaxe

Regardez par la fenêtre et prenez l’arbre le tronc de l’arbre le plus proche. Ah là déjà il y a un piège, vous devez me dire “comment savoir si c’est le plus proche ?”. Si vous êtes en ville, regardez un lampadaire. Si vous n’avez aucun des deux, prenez votre doigt. Bon en fait c’est de la triche avec le doigt, parce que vous avez un sens non relié à la vue qui vous donne une bonne idée de la position de votre doigt dans l’espace. Ainsi, si vous fermez les yeux vous pouvez ainsi aisément arriver à toucher votre nez et à savoir à quel moment exact votre doigt va toucher votre nez. Bon là je fais une petite pause pour que tout le monde puisse se toucher le nez. C’est ce qu’on appelle la proprioception. Il y a une vidéo de e-penser sur les sens que l’on a en plus des 5 sens habituels. Bref, je dérive du sujet. Revenons à notre arbre. Maintenant vous allez fermer un oeil, puis l’autre alternativement. Si vous êtes en voiture, vous le ferez après être arrivé. Si vous pilotez un avion de chasse, je vous ai déjà dit d’arrêter de déconner. Normalement, vous voyez votre arbre bouger. Mais en vrai, il n’a pas bougé hein, c’est juste que vous le regardez avec deux points de vue différents. Plus l’objet est loin, moins il va bouger entre les deux images, plus l’objet est proche, plus il va bouger entre les deux images.

On peut maintenant associer un angle à ce mouvement. Cet angle, c’est celui entre les deux droites partant de l’arbre et allant à vos deux yeux. Dis différemment, parce que je sais que beaucoup de gens ont été traumatisés par la trigonométrie quand ils étaient petits, imaginez que quelqu’un se trouve au pied de l’arbre, et qu’il regarde spécifiquement votre oeil droit a travers une longue vue, de quel angle doit il tourner la tête pour observer votre oeil gauche. Cet angle, votre cerveau est capable de l’estimer à partir du déplacement de l’objet d’une image à l’autre (c’est pas très compliqué, je ferais un dessin). Cet angle, bien évidement, est lié à la distance entre vous et l’arbre et la distance entre vos yeux.

Et je pense que vous ne le saviez pas, mais votre cerveau est capable de faire de la trigonométrie beaucoup plus rapidement que vous, parce qu’avant même que vous ayez eu le temps de réciter tangente = cote adjacent sur coté opposé, attends non c’est le contraire, merde attends je vérifie sur Wikipédia… votre cerveau a déjà eu le temps de vous dire que l’arbre se trouve à peu près a tel distance. Il a utilisé la bonne formule de trigonométrie et il connait aussi en mémoire la distance entre vos yeux (environ 3.5 cm). Alors il ne va pas vous donner une distance en mètres hein, mais si vous foncez sur le lampadaire, il va être capable de vous dire ”là, tu vas te le prendre”. Ou si vous tendez la main vers un objet, il va vous dire comment tendre le bras si vous voulez atteindre l’objet, juste ce qu’il faut pour pas le taper. Où tout simplement, il va être capable de faire la mise au point de l’oeil sur cet objet pour le voir net.

C’est ce qu’on appelle la vision stéréoscopique. Apparemment 2% de la population (excluant les non-voyants) serait stéréo-déficient. Les humains ne sont pas les seuls  avoir cette capacité, mais pas tous les animaux ne l’ont. En particulier, parce que avoir les yeux l’un à coté de l’autre ne permet pas de voir grand chose, contrairement aux animaux qui ont les yeux sur les cotés de la tête. On a un peu un compromis entre la taille du champ de vision et la possibilité d’avoir les deux yeux qui regardent la même chose pour avoir la stéréoscopie et la mesure des distances. Enfin, on a l’exemple du caméléon qui est un animal fascinant car il a les yeux monté sur tourelle, ce qui lui permet de les bouger indépendamment les yeux verticalement ou horizontalement, mais aussi de les pointer vers l’avant pour avoir de la stéréovision. Bon pour conclure, vous aller peut être me dire “ah mais ouais, mais les borgnes ne se prennent pas des lampadaires tous les jours dans la rue”, et là je vous dit qu’il y a aussi sans doute d’autre manière d’évaluer des distances, par exemple en faisant l’inverse, c’est à dire en connaissant à peu près la taille de l’objet que vous regardez (largeur du lampadaire = bah souvent c’est 20cm environ), vous pouvez aussi en déduire une distance, avec un seul oeil. Vous faites une hypothèse sur la taille de l’objet, qui vous donne une estimation de la distance.

Bref, je pense que c’est que la stéréoscopie, n’est pas la seule manière dont notre cerveau évalue les distances. Mais en astrophysique, on n’a pas le choix ! Parce qu’une étoile, même avec le plus gros télescope au monde c’est toujours un point, donc ce n’est pas possible de dire “alors j’estime qu’elle fait cette taille là et j’en déduis sa distance”. Ou alors pour les objets dont vous pouvez résoudre, comme les photos de galaxies de Hubble par exemple, et bah vous êtes emmerdés parce que la première fois que vous voyez ça, vous n’avez aucune idée de sa taille en fait… du coup vous êtes obligé d’utiliser la parallaxe pour avoir une distance.

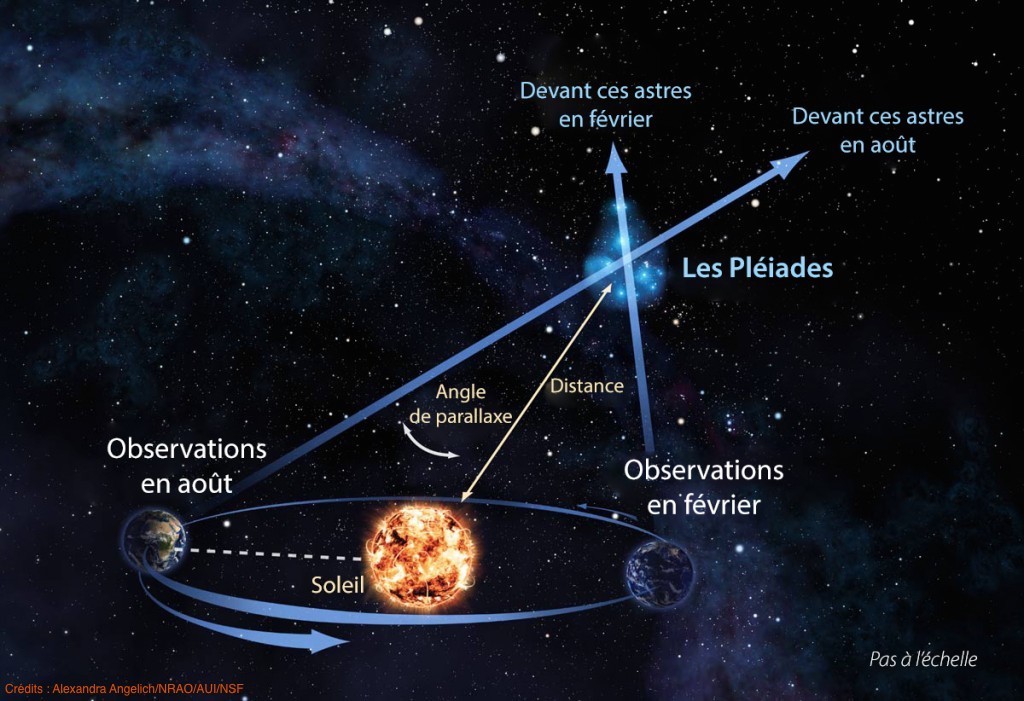
Et donc c’est le même système, sauf que vous avez besoin d’une base beaucoup plus grande qu’entre vos deux yeux ! Et une bonne base, c’est la distance Terre Soleil. Donc votre oeil droit, c’est la photo que vous prenez du ciel le 21 juin et votre gauche, c’est la photo que vous prenez du ciel le 24 décembre. Entre les deux, vous savez que vous avez bougé de 2 distance Terre Soleil soit 3.10^11 mètres. J’ai introduit tout à l’heure une unité parfaite pour ça, la distance Terre-Soleil ou unités astronomique. Donc voila, votre base d’observation, la distance entre vis yeux, la base du triangle, c’est 2 unités astronomiques. Et à partir du mouvement des astres au 21 juin et au 24 décembre, vous allez pouvoir en déduire la distance de l’étoile que vous observez ! C’est ce qu’on appelle la parallaxe. Enfin c’est 2x la parallaxe, pour se ramener à une base de 1 unité astronomique (voir schéma plus haut).

Donc si une étoile a bougé d’un degré entre le 21 juin et le 24 décembre, vous en déduisez que votre parallaxe est 0.5 degrés  et qu’elle se trouve à 114 AU. Bon mais en fait 1 degrés, c’est énorme, les étoiles sont tellement loin que leur angle parallactique est bien plus petit ! L’étoile la plus proche de la Terre, celle qui a l’angle parallactique le plus important est de 768 milli-secondes d’arc. Je fais une pause. Tout le monde sait ce que c’est qu’un degré. Alors les degrés, on n’a pas de système décimal pour cette unité (encore un coup des anglais), donc le degré se décompose en 60 minutes d’arc. Et chaque minute d’arc se décompose en 60 secondes d’arc. Et à partir d’ici, on repasse en décimal (simple hein !) et on a donc des milli-secondes d’arc, qui sont un millième de seconde d’arc. Donc 1 milli seconde d’arc, c’est… 1degré, divisé par 60, divisé par 60, divisé par 1000. Donc 768 milli-secondes d’arc, c’est 0.0002 degrés ! Et c’est là qu’on voit que l’astrométrie, c’est une science de gens précis. En gros vous allez noter la position des étoiles tous les jours et regarder si elle a bougé d’un poil de micropouillèmes.

On retient les noms des grands malades qui ont littéralement passé leur vie à calculer des pouillèmes de degré dans le ciel tous les jours, parmi lesquels Hipparque et Tycho Brahé. Ces mecs là ont tout de même réussi à me faire dire que parfois le boulot d’astronome est le plus chiant au monde, et c’est mon boulot ! Mais en plus, ils n’ont pas réussi à calculer de distance d’étoiles !

Première parallaxe d’étoiles

Le problème, c’est que si l’objet est trop loin, on arrive plus à mesurer un angle. Essayez en fixant un objet très loin et en fixant un oeil puis l’autre, vous ne devriez pas voir l’objet se déplacer d’une image à l’autre… Et bien c’est la même chose pour les étoiles : si l’angle est trop petit, et bien on ne peut plus faire de parallaxe. Et en outre, l’atmosphère fait bouger un peu les étoiles, du coup on n’est pas trop précis depuis la Terre. Et c’était même un des arguments de Tycho Brahé contre Copernic. Si la Terre tourne autour du Soleil, alors les étoiles devraient avoir une parallaxe. Ou alors c’est qu’elles sont vraiment tellement loin qu’elles ne bougent pas ! Mais Tycho Brahé n’a pas pu faire ce saut. Pour lui ce n’était pas possible qu’il y ait une telle différence de distance entre l’orbite de Saturne, la planète la plus éloignée à l’époque et celle des étoiles. Du coup il va proposer un modèle un peu bâtard, où la Terre est immobile, le soleil, la Lune et les étoiles tournent autour de la Terre, et les autres planètes tournent autour du Soleil. Tout le monde ne peut pas faire de révolutions scientifiques non plus.

Par contre, certains auteurs antiques, adeptes de l’héliocentrisme n’ont pas hésité devant l’absence de mouvement des étoiles ! Et cela nous donne notre première estimation de la soirée de la taille de l’univers ! En prenant le modèle héliocentrique, d’Aristarque de Samos, Archimède fait une estimation de la taille de l’univers. On en avait déjà parlé dans l’épisode #145 de Podcast Science, où Robin nous a parlé d’infini. En effet Archimède s’attaque dans un traité à la question “y a t’il un nombre infini de grains de sable dans l’univers” Du coup pour ça, il se lance dans le calcul du nombre de grains de sable de l’univers (allons y gaiment). Et il dit non, puisque le grain de sable a une taille non nulle et que l’univers à une taille fini, on a donc un nombre fini de grains sable. Bon, mais pour compter des grains de sables, il est bien obligé de faire une estimation de la taille de l’univers. Bon alors je rentre pas dans le détail, mais il remarque le fait que la sphère des étoiles fixes, donc l’univers est au moins assez grand pour que les étoiles “ne bouge pas” dans le modèle des étoiles. Ce n’est pas super clair, mais je vous lis l’extrait :

Tu sais que le monde est appelé par la plupart des astronomes une sphère dont le centre est le même que celui de la terre et dont le rayon est égal à la droite placée entre le centre de la terre et celui du soleil. Aristarque de Samos rapporte ces choses en les réfutant, dans les propositions qu’il a publiées contre les astronomes. D’après ce qui est dit par Aristarque de Samos, le monde serait beaucoup plus grand que nous venons de le dire; car il suppose que les étoiles et le soleil sont immobiles ; que la terre tourne autour du soleil comme centre; et que la grandeur de la sphère des étoiles fixes dont le centre est celui du soleil, est telle que la circonférence du cercle qu’il suppose décrite par la terre est à la distance des étoiles fixes comme le centre de la sphère est à la surface.

Archimède, dans L’arénaire

Mais en gros l’argument principal c’est: la terre tourne autour du soleil, donc puisque les étoiles ne bougent pas, c’est qu’elles sont sacrément loin. Bon il donne une estimation de la Taille de l’univers 130’000 unités astronomique (ce qui est, on va le voir, inférieur à la distance à la première étoile). Cette estimation va grandir, grandir au fur et à mesure que la précision des instruments augmente : si vous êtes capable de mesurer un angle deux fois plus petit que l’angle de votre prédécesseur, et que les étoiles ne bougent toujours pas, c’est donc que les étoiles sont encore au moins deux fois plus loin. Et ainsi de suite…

Le physicien allemand Bessel arrive à mesurer la première parallaxe en… 1838.  Donc voila, on peut rire de la mythologie nordique mais on a calculé notre première distance il y a 180 ans. Et là je sais pas si vous imaginez, mais partir du moment où on peut calculer les distances, les étoiles ne sont plus sur une sphère, le papier peint de l’univers, mais à différents endroits. D’un coup l’univers devient 3D ! Et pourquoi c’est super important ? Parce que connaitre la distance, comme pour notre cerveau permet de nous transporter là bas en imagination. Si vous connaissez la distance et la luminosité apparente qui vous parvient de l’étoile, vous pouvez calculer la luminosité réelle de l’étoile. Vous répondez à la question “est ce que c’est une étoile peu brillante mais près où une étoile très brillante mais loin”. Vous transformez les caractéristiques apparentes en caractéristiques réelles de l’étoile ! Et si vous avec de bons modèles d’évolution stellaire, vous pouvez déduire l’âge de l’étoile, et sa masse et son rayon, et pas mal d’informations à partir de sa luminosité propre. Mais ce n’est possible que si vous avez la distance. Sans distance, vous ne pouvez rien !

Parsec et année lumière

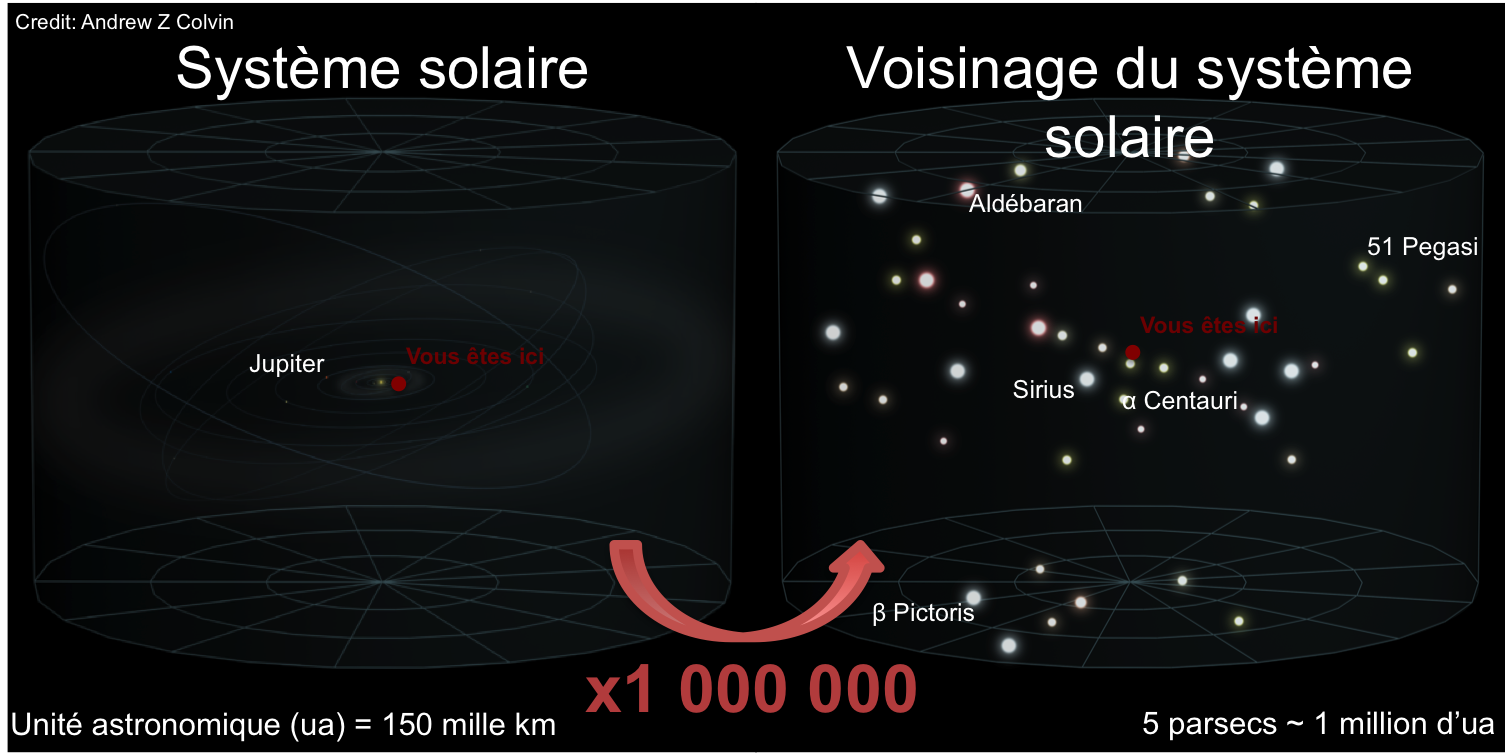
Ok pour vous donner une idée des distances, parlons de l’étoile la plus proche de nous, Proxima du Centaure. En utilisant la parallaxe, on peut déduire que la distance de cette étoile est de 206’000 unités astronomiques. 206’000 distance Terre-soleil pour notre voisine la plus proche. On voit que l’unité astronomique n’est pas vraiment l’unité en vigueur ici. Donc on va devoir changer. On va donner deux unités de longueur différentes. Celle utilisée par les astronomes est le parsec. Elle est complétement déduite de la parallaxe dont je viens de parler. Parsec, c’est une unité qui dit : si la parallaxe (l’angle) vaut 1 seconde d’arc, alors votre objet est à 1 parsec. Parallaxe d’une Seconde d’arc. PAR-SEC. Etymologiquement, on ne peut pas faire plus simple. On voit par exemple que la parallaxe de Proxima du centaure était de 768 milli-secondes d’arc, soit un tout petit peu moins d’une seconde d’arc. Donc elle est située à un tout petit peu plus d’un parsec. Je rappelle pour ceux qui sont un peu perdus : plus l’étoile est loin, plus l’angle qu’elle semble faire est petit (comme les arbres et vos deux yeux) ! Donc la parallaxe de Proxima du centaure est à petit peu moins d’une seconde d’arc. Donc elle est située à un tout petit peu plus d’un parsec : 1.3 parsec. Un parsec correspond à 3 x 10¹³ km.

Une autre unité, c’est l’année lumière. Une années lumière c’est la distance que parcourt la lumière en une année, c’est à dire 5.9 x 10¹² km. Proxima du centaure est à 4.2 années lumière. 1 parsec, c’est 3 années lumière pour vous donner une idée. En vrai, l’année lumière est pas vraiment utilisée par les astrophysiciens, sauf peut être par ceux qui s’intéressent à l’âge de l’univers, et encore, c’est plutôt une unité grand public, on compte plutôt en parsec. Contrairement à pas mal de gens qui font de la vulgarisation et même de la très bonne, je vais compter en parsecs pour la suite. C’est pas seulement pour me la péter, c’est aussi parce que contrairement à l’année lumière, qui ne me parle pas du tout perso, 1 parsec correspond a peu près à la distance de nous à l’étoile la plus proche. Ce qui nous donne une petite idée des distances à chaque étape. Attention à bien se le rappeler.

A ce jour, on a découvert 65 étoiles entre donc 1.3 parsec (la plus proche, Proxima du Centaure) et 5 parsecs de nous par exemple (voir liste ici). Je dis à ce jour, parce qu’on a encore trouvé une étoile à seulement 4.5 pc en 2014. Il existe en effet des naines brunes, des objets tellement peu lumineux que l’on peut encore aujourd’hui en trouver des relativement proches. Ces 65 étoiles sont dans ce qu’on appelle le voisinage interstellaire du soleil. Depuis la Terre ferme, on arrive à mesurer des distances jusqu’à 40 parsecs, c’est a dire 130 années lumière. Pour vous donner une idée de à quel point c’est pitoyable, le centre de la galaxie est à 8.34 kiloparsecs ! 8340 parsecs ! En gros, depuis la Terre ferme, on arrive à mesurer la distance de quelques milliers d’étoiles.  Et on en était bloqué là jusqu’en 1989.

Un télescope spatial a permis une révolution dans ce domaine, c’est Hipparcos. Ce télescope européen a scruté entre 1989 et 1993 et a fait passer le nombre de parallaxe mesurée de 7000 à 118 218 ce qui a donné le catalogue Hipparcos. Ca a permis de cartographier le voisinage comme jamais auparavant ! Le successeur Hipparcos, c’est la mission astrométrique Gaia. Elle a été lancée en 2013 et devrait donner la position de plus d’un milliard d’étoile et une distance précise à moins de 1% pour 20 millions d’entre elles. On va apprendre des tas de trucs sur la galaxie avec ça. Aussi, elle devrait trouver des milliers d’exoplanètes…

Intermède : Science Fiction et anthropocentrisme

Bon petite pause dans les grands chiffres. Je ne sais pas si vous avez remarqué mais les unités que je vous donne depuis le début sont complètement centrées sur l’humain. Alan nous avait définis le mètre dans les épisodes de Podcast Science 117 et 118, et initialement, ça correspond arbitrairement à un quarante-millième de la distance à l’équateur. Si votre planète est un poil plus grande, alors votre mètre n’est plus le même. L’unité astronomique, ça dépend de la distance Terre Soleil. Mais bon si vous êtes martien, ce n’est pas l’unité que vous choisiriez normalement. Encore plus si vous vivez autour d’une autre étoile. Le parsec est lié à cette distance Terre Soleil, car il est relié à l’angle parallactique de l’étoile observée. Même l’année lumière est liée à l’année terrestre. Mars, par exemple, tourne autour du soleil en 687 jours, ce qui fait que si un martien définissait une année martienne lumière, elle serait environ 2 fois plus grande que l’année lumière que nous utilisons. Plusieurs remarques sur ça :

1. C’est pas forcément grave pour le moment vu que les seuls gens avec qui ont discutent sont terriens. Si vous voulez discuter avec d’autres gens, voir mon épisode podcast science #189 sur les sondes Voyager sur le message aux aliens.
2. Méfiez vous des mecs qui vous trouvent des coïncidences bizarres dans la taille des pyramides et qui vous explique que c’est les aliens. Les aliens, par définition ne sont pas ethnocentrés. Donc quand dans le documentaire La révélation des pyramides (vous pouvez le trouver sur youtube, c’est très drôle) on vous explique que la taille de la pièce mortuaire divisée par je sais plus quoi donne très exactement la vitesse de la lumière en m/s, cela doit faire tilt dans votre tête. Ni les aliens ni les égyptiens ne savent ce que c’est qu’un mètre ou une seconde, parce que ces unités ont été inventées totalement arbitrairement des millénaires plus tard. Et qu’elles ne représentent pas grand chose pour quelqu’un qui n’a pas la même culture que vous.
3. Pour les fans de Science fiction, un extrait :

Il y a deux erreurs dans cet extrait ! Alors la première erreur, celle que tout le monde remarque sur internet, c’est que Han solo utilise une unité de distance comme une unité de temps (les fans intègrent cette erreur au scénario en disant qu’Obi-Wan devine à ce moment qu’Han est un plaisantin, ce qui se voit à son visage atterré). Mais la deuxième erreur, c’est que dans une galaxie far far away où est censé se passer l’action, un parsec n’a pas vraiment de sens, il n’a de sens que si on est sur Terre. Dans Le cycle Fondation d’Asimov, situé dans notre galaxie et dans un futur très lointain qui a oublié la Terre, ils comptent aussi en parsec, mais je crois me souvenir qu’Asimov est justement assez malin pour en faire un artefact préhistorique dont personne ne connait la signification. A vérifier.

Vitesse et Effet Doppler

On a vu qu’elles sont les positions des étoiles autour de nous, mais qu’elles sont leur vitesse ? On va devoir séparer la vitesse perpendiculaire à nous et la vitesse dans notre direction. Pour les vitesses perpendiculaires à nous, c’est-à-dire dans les directions gauche-droite ou haut-bas, ils suffit de les regarder bouger et de regarder de combien elles ont bougé en un an exactement (c’est à dire au moment où la Terre n’a pas bougé). C’est à dire que l’on va calculer le mouvement dans le ciel qui n’est pas celui du au mouvement de la Terre, mais bien au mouvement propre de l’étoile. Si vous connaissez leur distance, vous pouvez en déduire le nombre de km qu’elles ont parcourues en un an et donc la vitesse. Par exemple, l’étoile de Banard, étoile la plus proche du soleil après les 3 étoiles du Système Centauri : elle bouge à une vitesse de 90 km/s en vitesse transverse. Encore une fois si vous n’avez pas la distance de l’étoile, vous pouvez mesurer sa vitesse apparente dans le ciel, mais pas sa vraie vitesse.

Qu’en est il de la vitesse dans votre direction ? C’est à dire qui s’éloigne ou se rapproche de nous. Et bien là on va utiliser l’effet Doppler, le même que pour les radars des voitures. L’effet Doppler désigne le décalage de fréquence d’une onde (mécanique, acoustique, électromagnétique ou d’une autre nature) observé entre les mesures à l’émission et à la réception, lorsque la distance entre l’émetteur et le récepteur varie au cours du temps. Du coup vous prenez une raie que vous connaissez dans votre spectre lumineux et qui se trouve à la position A. Par exemple, la célèbre raie Lyman-alpha de l’hydrogène se trouve normalement exactement à 121.567 nm. Et là elle se trouve, par exemple, à la position A+1% ou A-1%. En fonction de ce décalage, vous pouvez en déduire la vitesse immédiatement de l’astre dans votre direction. Voir la vidéo de Science4All sur la question. Toujours pour la vitesse de l’étoile de Banard, on déduit une vitesse dans notre direction de 111 km/s. Du coup, au total, sa vitesse par rapport au soleil est de 142 km/s. On se rappelle que la vitesse de la Terre par rapport au soleil est de 30 km/s, on a encore passé une étape. L’étoile qui la vitesse la plus rapide par rapport au soleil à ce jour parmi les étoiles proche est Wolf 424, qui se déplace à 555 km/s, par rapport au soleil.  

La Voie lactée

Zeus, voulait rendre son fils Héraclès immortel. En fait, il l’avait eu lors d’une de ses nombreuses relations adultères, avec une mortelle, Alcmène. Du coup, il essaye en douce de lui faire téter le sein d’Héra, sa régulière. Celle ci se réveille et comprend que son mari la prend pour une conne et une station service en prime. Elle essaie alors d’arracher le bébé à son sein. En se faisant, elle laisse échapper une giclée de lait qui se répand dans le ciel. Voilà encore une cosmogonie pour nous décrire l’existence de la voie lactée. Et pendant qu’on est dans l’ethnologie, devinez comment on dit voie lactée en grec : γαλαξίας, galaxias, qui a donné galaxie.

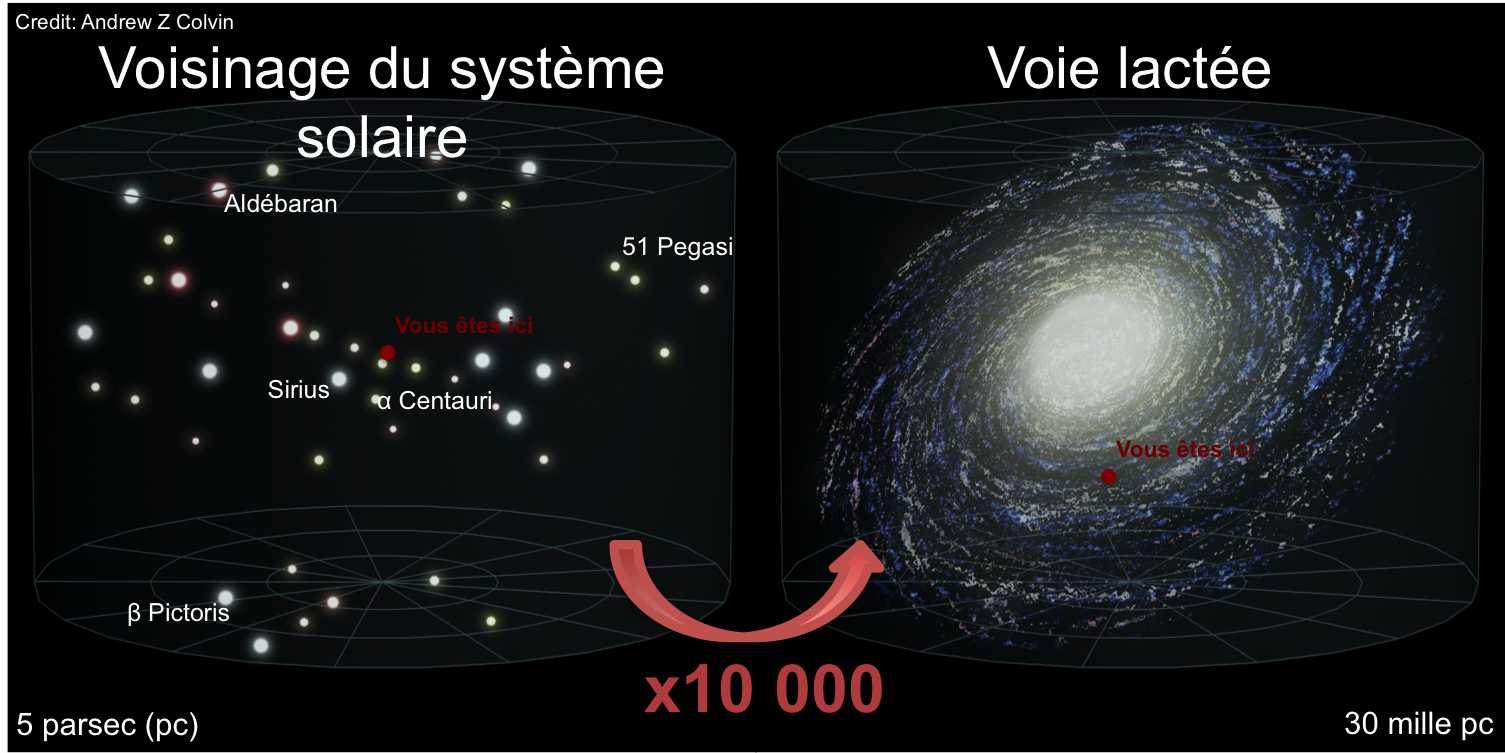
Bon comme on le voit on en est maintenant avec une position et une vitesse pour certaines (moins de 1%) des étoiles de notre galaxie. En étudiant les hausses de densité locale d’étoiles dans la galaxie,  Harlow Shapley put déterminer vers 1918 la position du centre de la galaxie et en déduire sa taille approximative. En étudiant les différentes rotations des étoiles et leur distance au centre, d’autres purent en déduire que la galaxie étaient plutôt spirale. En utilisant les parallaxes pré Hipparcos dont je viens de vous parler, on a pu ainsi commencer à deviner un bras, puis 2, puis 3 dans les années 50. La galaxie, comme la sphère des étoiles, devient 3D. En comparant avec d’autres images de galaxie, on a réussi à achever de se convaincre que nous sommes dans une galaxie spirale, d’environ 30 kpc, soit 30’000 parsec. Le soleil se trouve à 8.6 milliers de pc du centre. Du coup, les étoiles les plus éloignées de notre soleil dans la galaxie se trouvent à environ 24 milliers de pc (ils faut aussi compter que certaines étoiles sortent un peu du plan). Pour rappel, l’étoile la plus proche du soleil, Proxima du Centaure, se trouve à seulement 1.3 pc, ce qui représentait 206’000 distance terre-soleil. Donc la distance entre le soleil et le centre de la galaxie est plus d’un milliard de fois plus grande que la distance Terre-Soleil. On peut aussi donner la vitesse du soleil lors de sa rotation autour du centre de la galaxie est 240 km/s.

Comme dans le système solaire, on aurait pu s’attendre à ce que les vitesses des étoiles et leur distance au centre de la galaxie soient reliées par les lois de Kepler. On a cependant vérifié que ce n’est pas le cas, dans notre galaxie et d’autres, ce qui suggère la présence de masse cachée, que l’on a appelée matière noire, qui désigne donc de la matière, responsable de la grande majorité de la masse des galaxies et dont on ne sait… rien à l’heure actuelle.

Chandelles et Céphéides

Bon mais il reste tout de même plusieurs soucis pour aller plus loin. Comment faire si votre objet est toujours trop loin pour avoir une parallaxe ? On a vu qu’on pouvait à peine mesurer la distance de 20 millions d’étoiles dans la galaxie, qui en contient plus de 200 milliards. On fait comment pour le reste ? C’est là qu’entre en jeu une longue suite de chandelles standards. Avant de continuer, je dois définir ce qu’est la luminosité absolue ou réelle, par opposition à la luminosité apparente. La seconde est claire, c’est celle que vous recevez depuis la Terre, qui est donc facile à calculer. Mais la même étoile en fonction si elle est située à 1 parsec ou 2 parsec, va avoir une luminosité apparente différente. C’est pour cela qu’on va parler de luminosité réelle, qui est la luminosité si vous êtes collé à elle. Mais pour la plupart des objets, si vous n’avez pas la distance, vous n’avez pas accès à la luminosité réelle. Les chandelles standards sont donc des objets particuliers dont on connait exactement la luminosité propre. Si vous connaissez leur luminosité propre et que vous mesurez avec un télescope leur luminosité apparente, vous pouvez en déduire leur distance ! Je ne vais parler que des deux type de chandelles standards : les céphéides, qui vont servir dans la galaxie et dans les galaxie proches, et les supernovae de type Ia pour les distances un peu au delà.

Les céphéides sont des étoiles variables, c’est à dire que leur luminosité varie au cours du temps. Mais une astronome nommée Henrietta Swan Leavitt découvrit une propriété particulièrement intéressantes des céphéides dans les années 1900. Elle étudia ces étoiles en regardant les quelques distances par parallaxe disponibles à l’époque. En connaissant leur distance, vous pouvez donc vous transportez en imagination à coté, et en déduire la luminosité réelle de l’étoile ! Et là elle s’aperçut que cette luminosité réelle est reliée à la période de variation de l’étoile par une relation. Du coup, en calibrant bien cette relation, elle avait une formule qui donnait, pour toute étoile de type céphéides sa distance en fonction de la période de variation de sa luminosité. Ainsi en utilisant cette relation vous pouvez donner des distances de plusieurs milliers de parsecs et le ciel prend encore de la profondeur. Voilà votre chandelle.

Groupe local

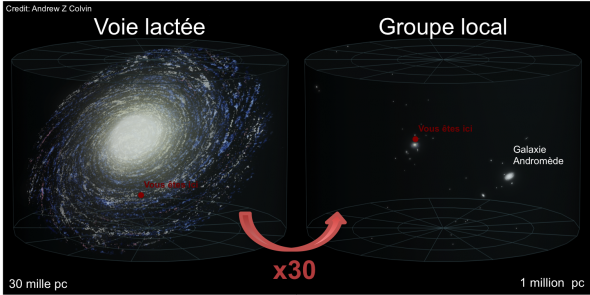
Cette relation a permis à Edwin Hubble pour la première fois de regarder dans un télescope et de dire : ces machins nébuleux que l’on voit, ils sont en fait situés à plusieurs centaines de milliers de parsecs. Pour rappel, la voie lactée fait 30 milliers de parsecs. Elles sont donc situées en dehors de la galaxie. Ce sont en fait d’autres galaxies ! A quelle distance sont ces galaxies ? Les plus proches sont les deux nuages de Magellan et elles sont tellement proches de la voie lactée (48 milliers de parsecs et 60 milliers de parsecs) qu’on pense qu’elles en sont satellites. Ensuite Andromède est la galaxie spirale la plus proche de nous. Elle est située à 780 milliers de parsecs. Elle contient 1000 milliards d’étoile et est donc un peu plus grosse que la galaxie. Elle fonce vers nous à 300km/s. Elle devrait nous rejoindre d’ici 4 milliards d’années. Cependant, on l’a vu les distances entre étoiles sont gigantesques en comparaison des distances dans les systèmes stellaires et a fortiori des tailles des étoiles. Du coup, le risque de collisions des étoiles entre elles est faible. D’ici 7 milliards d’années ces galaxies devraient former une seule et même galaxie.

Ces galaxies et 30 à 40 autres forment ce qu’on appelle le groupe local. La distance typique entre ses galaxies est la centaine de milliers de parsec. Là on passe à la taille d’au dessus car le groupe local est étendu d’environ 3 millions de parsec, à comparer au 30’000 parsec de la galaxie, à comparer au 1.3 parsec de la distance Soleil-Proxima du Centaure. 3 millions c’est à peu près la distance maximum auxquelles les céphéides nous permettent d’accéder. En effet au delà ces étoiles deviennent trop faibles pour servir de chandelles. C’est en utilisant ces chandelles que Hubble a trouvé sa loi (que Georges Lemaitre avait aussi intuitée). Il s’est aperçu que plus les galaxies s’éloignaient de nous, plus elles avaient un décalage de leur lumière vers le rouge. En fait, ce n’est pas vraiment l’effet Doppler lumineux dont on a parlé dans l’épisode précédent, mais un effet relativiste de l’expansion de l’univers, mais qu’on peut interpréter pareil pour les objets les plus proches. J’en ai parlé au début de mon épisode de Podcast Science sur Hubble. Du coup, cette loi de Hubble a permis de montrer que l’univers était en expansion, ce qui permit pour la première fois de donner un âge à l’univers vers la fin des années 20.

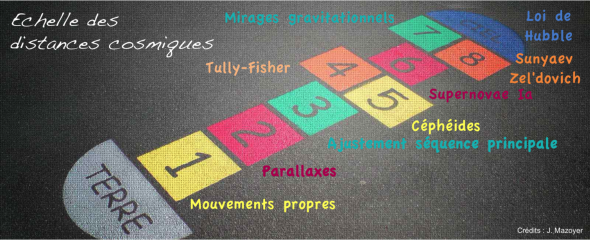
Echelle des distances cosmiques et Supernovae de type Ia

Mais vous comprenez pourquoi on parle d’échelle des distances cosmiques. Vous devez connaitre très précisément la distance Terre Soleil. Une fois que cette distance est bien calculée, avec une bonne parallaxe des étoiles proches, vous avez une distance très précises pour ces étoiles et en particulier des céphéides. Une fois que vous êtes bien sur de cette distance pour plusieurs céphéides, vous pouvez affinez la relation distance-période et l’utiliser pour aller plus loin. Mais attention, un problème de mesure à un moment est terrible. Si votre échelon précédent n’est pas solide, tout ce que vous dites après est faux !

C’est ce qui est arrivé en 1952, quand Walter Baade a annoncé en conférence à Rome qu’en fait ce qu’on pensait être un unique groupe de céphéides était en fait de deux types qui ne se comportaient pas tout à fait pareil. Du coup on avait extrapolé les résultats d’un groupe aux deux à la fois. Heureusement, pas d’inquiétude, il avait refait l’étalonnage proprement. Bon, mais par contre, la distance à toutes les galaxies connues données par Hubble et la taille de la voie lactée donnée par Shapley prenaient un facteur 2 d’un coup. Le jour où la galaxie a doublé, vous imaginez la tête des mecs à la conférence. Et l’univers a pris un bon coup de vieux aussi dans la partie, vu que les estimations de son âge sont basées sur la distance des galaxies et leur éloignement. Mais c’est ce qui arrive fréquemment, c’est pour ça qu’on a besoin de beaucoup de méthodes indépendantes pour mesurer des distances et qui se recoupent pour mesurer des distances. Alors bon ça arrive pas tout les jours un facteur 2 dans la taille de l’univers, mais un affinage de quelques pour-cent dans la mesure de la distance ou du comportement de tel groupe d’étoiles peut avoir des conséquences sur la taille de l’univers entier ou sur son âge par exemple.

Deux autres échelons les plus connues (ou chandelles) de l’échelle des distances cosmiques sont, rapidement l’ajustement sur la séquence principale et la loi de Loi de Tully-Fisher. La séquence principale (voir schéma), c’est absolument fondamental en astrophysique, c’est le fait que la couleur de la plupart des étoiles et leur luminosité réelle suivent une courbe assez jolie, un peu tordue et assez bien connue. Du coup si vous connaissez la couleur de l’étoile, vous en déduisez sa luminosité réelle, puis comme vous connaissez sa luminosité apparente, vous avez sa distance. Ca c’est plutôt pour les distances d’étoile au sein de notre galaxie. Enfin la Loi de Tully-Fisher, c’est une une relation empirique établie entre la luminosité réelle d’une galaxie spirale et l’amplitude de sa courbe de rotation. Du coup selon comment elle tourne, vous avez sa luminosité réelle, puis comme vous connaissez sa luminosité apparente, vous avez sa distance. Bref, ces deux échelons, comme les céphéides ou les supernovaes de type Ia, nécessitent que l’on connaisse parfaitement les lois derrière, qu’on les ait calculées pour plein d’objets et bien étalonnées. Il faut utiliser l’échelon d’avant et prendre plein de mesures de distances et une fois que vous êtes bien ancré sur votre échelon, que vous êtes sur de vous, vous vous lancez et vous calculez la distance de plein objets en utilisant ce nouvel outil. Il faut bien se rendre compte que si l’on se plante de 10% sur un des échelons, ce sont tous les objets utilisant cet échelon où un autre au dessus qui prennent 10% et donc souvent, à terme, la taille de l’univers entier (et l’âge aussi par la même occasion).

Finalement le dernier échelon dont je vais parler, la dernière chandelle, mais il y en a d’autres sont les supernovaes de type Ia. Elles ont une importance particulière car elles ont permis de faire une découverte majeure. Ces étoiles en explosion ont une luminosité réelle qui peut être déterminé très précisément en étudiant la courbe de leur luminosité en fonction du temps. Comme pour les céphéides, on peut alors, si l’on a une luminosité réelle et une luminosité apparente, vous pouvez déduire une distance proprement et vous avez votre chandelle. On a utilisé ces chandelles dans les années 1990 pour affiner la loi de Hubble pour les galaxies les plus éloignées. A la surprise des astronomes, cet affinage a montré une accélération de la vitesse de l’univers au lieu d’un ralentissement comme on s’y attendait (qui a valu le prix Nobel aux astronomes concernés). Du coup, on a du trouver une explication, l’énergie sombre, pour expliquer cette expansion de l’univers. Elle est encore grandement méconnue, mais correspondrait à 68% de l’énergie totale de l’univers. Le domaine des distances en astronomie et des chandelles standards en particulier, que l’on appelle généralement astrométrie, est encore très très étudié en astronomie, il faut affiner encore et encore les mesures les modèles, ce qui permet à terme d’affiner les paramètres fondamentaux de l’univers. Finalement, une fois que vous êtes bien sur de votre loi de Hubble (qui relie le décalage vers le rouge à la distance des galaxies), vous pouvez l’utiliser comme dernier échelon pour les galaxies les plus lointaines de l’univers.

Super amas de la Vierge et Laniakea

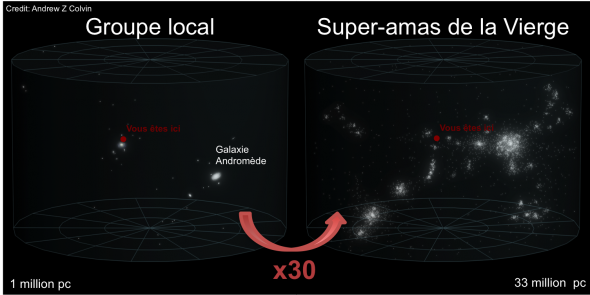
Ces estimations de distance ont permis de repérer d’autres groupes de galaxie. Le Groupe local forme un ensemble considéré comme typique de quelques dizaines de galaxies. Cet ensemble interagit faiblement avec ses voisins, comme le Filament du Sculpteur ou le Nuage des Chiens de Chasse (c’est mignon hein). Tous sont situés en périphérie d’un amas de galaxies (un amas, contrairement à un groupe a plutôt un nombre de galaxie supérieur à 100, voire 1000), appelé amas de la Vierge. Ces groupes et cet amas forment le super amas de la vierge dont nous faisons partie. Cet amas fait environ 33 millions de parsecs et il contient au moins 100 groupes ou amas de galaxies et environ 10’000 galaxies (contenant chacune entre plusieurs  milliards et plusieurs centaines de milliard d’étoiles). A cette échelle, les étoiles n’ont plus aucune importance, nous sommes à des distances un peu terrifiantes.

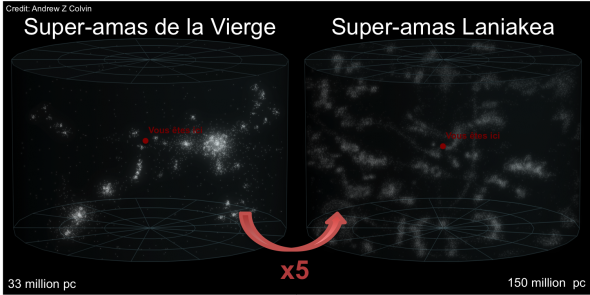
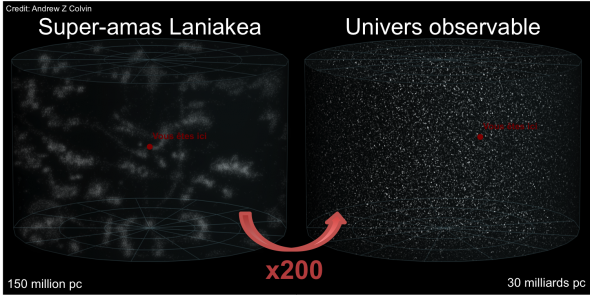
Encore au dessus se trouve Laniakea, découvert par  R. Brent Tully, de l’université d’Hawaï et Hélène Courtois, de l’université de Lyon I. Ce super-super amas fait environ 160 millions de parsecs de large. Pour rappel, je récapitule :

• l’étoile la plus proche du soleil, Proxima du Centaure, se trouve à seulement 1.3 pc, ce qui représentait 206’000 distance terre-soleil.
• la voie lactée fait 30’000 parsec et Andromède se trouve à 780’000 parsec.

Et je disais donc ce super-super amas fait environ 160 millions de parsecs de large…

Les chercheurs ont cherché à comprendre comment s’arrangeaient les super amas dans l’univers et ils ont trouvé qu’en fait ils ne sont pas par hasard, mais forment des longs filaments cosmiques. À ces échelles, on fait des simulations où chaque point représente plusieurs galaxies pour vous donner une idée.

Fin du voyage

On arrive à la dernière étape de notre voyage, enfin. A partir des estimations fines de la loi de Hubble on peut donc relier chaque décalage vers le rouge à une distance. C’est devenue la façon de compter les distances en fait. Alors une unité compliqué car elle dépend des estimations des paramètres de l’univers et aussi parce que définir des distances proprement à des échelles aussi grandes devient compliqué. Mais on peut retenir que un décalage vers le rouge de 1 est d’un ordre de grandeur de 1 milliards de parsec. Et là je sais pas si vous avez remarqué, mais on est tombé sur une unité de distance indépendante de nous, de notre planète, de notre étoile, de notre galaxie… Bon une distance pas vraiment utilisable pour des distances en dessous de l’intergalactique, mais tout de même.

L’univers observable, c’est l’ensemble des phénomènes observables par les astrophysiciens. En effet, l’univers à 13.8 milliards d’années, on ne peut pas voir d’événement plus anciens car leur lumières ne nous ai pas encore parvenue. Du coup l’univers observable est une sphère de 13.8 milliards d’années lumière de rayon et centre la Terre. Chaque point de l’univers à son univers observable qui peut, ou pas, intersecter l’univers observable de la Terre. Mais il faut aussi considérer que si un objet vous a envoyé de la lumière il y a 10 milliards d’années par exemple, et que vous avez pu constater qu’à ce moment il s’éloignait, vous pouvez en déduire l’endroit où il est maintenant. Il faut faire des hypothèses informées sur la vitesse d’expansion de l’univers, mais on peut en déduire la position actuelle des objets les plus lointains que vous observez, que l’on appelle horizon cosmologique. Et ils se trouve à 46.5 milliard d’années lumières, de nous. Du coup en diamètre de l’horizon cosmologique est de 90.5 Milliards de parsecs.

Conclusion

Qu’est ce qu’on doit retenir de notre voyage ? Déjà cette idée d’échelle des distances cosmiques. Le savoir en astronomie est difficile à acquérir, on ne peut pas faire d’expérience, on doit en permanence se demander si les objets sont loin ou s’ils semblent loin. J’avais utilisé, dans mon dossier sur les exoplanètes, l’analogie du phare que vous voyez briller au loin alors que vous êtes sur un bateau. D’une information lumineuse que vous savez partielle, on doit déduire toutes les informations (la distance du phare, la présence de récifs ou même le nom de l’île sur lequel il est situé). Du coup, on a construit une échelle, qui nous permet d’accéder à des distances dingues en commençant petit (le rayon de la Terre, la distance Terre-Soleil) pour finir aux galaxies les plus éloignées.

La deuxième chose sur laquelle je voulais insister, c’est la faible densité de l’univers au niveau des galaxies par rapport au reste. Si l’on prend les étoiles proches, vraiment la proche banlieue, disons 5 parsecs, ce qui fait 65 étoiles comme je le disais la dernière fois… soit rien du tout au sens de la galaxie. La porte à coté ! Et bien le rapport entre la  distance Terre-Soleil et ces 5 petits parsecs est le même qu’entre la voie lactée et… l’univers observable tout entier : 1 million. Ca tient au fait que la matière au niveau des étoiles et des planètes est super dense comparée au reste de l’univers. Alors il y a un énorme avantage, c’est que les galaxies passent leur temps à s’emplafonner les unes les autres mais que la probabilité que étoiles se rentrent dedans est super faible. Et ça c’est énorme pour le développement de la vie ! Si les étoiles se tamponnaient tous les 3-4 milliards d’année comme les galaxies, on n’aurait pas de vie intelligentes sur Terre. Par contre, le désavantage, c’est que sur 65 étoiles, la probabilité d’une autre planètes habitables dans les 65 étoiles qui nous entourent est faible, très très faible. Et que donc les distances pour aller sur une autre planète habitables seront forcément… astronomiques.

PS: Univers qui s’enfuit

On pourrait s’arrêter là, nous avons répondu à la question “où sommes nous”. Mais je continue encore un tout petit peu sur cette notion d’univers observable. L’univers est en expansion, on l’a vu. Cela veut dire que tous les objets s’éloignent de nous, et plus ils sont loin, plus ils s’éloignent vite. Jusqu’à aller plus vite que la lumière ? Oui bien sur, certains objets  subissent une expansion supérieure à la vitesse de la lumière, et cela signifie qu’ils deviennent invisibles à nous, car les photons émis vers nous, limité dans leur propagation à la vitesse de la lumière, ne pourront jamais nous parvenir. Par exemple, j’avais parlé dans mon épisode sur Hubble de l’ultra deep-field, cette image prise par le satellite Hubble, où on a fixé le ciel pendant 11 jours en cumulé pour atteindre les objets les plus reculés (E-penser en a fait une vidéo). Et bien les mesures de leur décalage vers le rouge montre que 40% des objets de cette image ne sont plus accessibles aujourd’hui : la lumière qu’ils nous envoient en ce moment même n’atteindra jamais la Terre, et dans quelques milliards d’années, ils disparaitront tout simplement en rougissant de plus en plus. Mais finalement que veux dire que l’expansion de l’univers est accélérée ? Et bien que de plus en plus d’objets basculent au delà de cette limite, et sont condamnés à disparaitre à terme.

Quand je considère la petite durée de la vie, absorbée dans l’éternité précédente et suivante, le petit espace que je remplis, et même que je vois, abîmé dans l’infinie immensité des espaces que j’ignore et qui m’ignorent, je m’effraie et m’étonne de me voir ici plutôt que là, pourquoi à présent plutôt que lors. Qui m’y a mis ? Par l’ordre et la conduite de qui ce lieu et ce temps a-t-il été destiné à moi ? […]

Pourquoi ma connaissance est-elle bornée ? Ma taille ? Ma durée à cent ans plutôt qu’à mille ? Quelle raison a eue la nature de me la donner telle, et de choisir ce nombre plutôt qu’un autre, dans l’infinité desquels il n’y a pas plus de raison de choisir l’un que l’autre, rien ne tentant plus que l’autre ?

Combien de royaumes nous ignorent !

Le silence éternel de ces espaces infinis m’effraie.

Blaise Pascal, issu de son texte Les deux infinis :

Quelques références :

La vidéo de Science4All sur l’effet Doppler en  Astronomie

La cosmologie (les grandes grandes distances de l’univers), c’est pas vraiment ma came, donc allez plutôt trainer du côté de ces gens là:

Start with a bang:  disappearing universe : https://medium.com/starts-with-a-bang/the-disappearing-universe-d7447467c63a

et  Is our Universe escaping us? https://medium.com/starts-with-a-bang/ask-ethan-69-is-our-universe-escaping-us-13960a2e45b7

E penser : 10 choses a savoir sur l’univers: https://www.youtube.com/watch?v=ItffNZtUYXA

Une jolie simulation : A Flight Through the Universe, by the Sloan Digital Sky Survey https://www.youtube.com/watch?v=08LBltePDZw