Commençons par ce qui paraît presque être la définition du hasard : une partie de pile ou face. Que peut-on en attendre ? On sait a priori qu’il y a une chance sur deux d’obtenir l’un ou l’autre résultat. Le « bon sens » nous dit : pour peu que l’on joue assez longtemps, il y aura à peu près autant de pile que de face.

Attention ! Pour cela, il faut déjà préciser que l’on suppose qu’il y a « équiprobabilité », c’est à dire autant de chance d’obtenir pile et face. Toutes les expériences dans lesquelles le hasard intervient n’ont pas des résultats équiprobables, loi de là, et il est parfois difficile d’estimer la probabilité d’un événement.

Quelques exemples simples de non équiprobabilité :

• Si on lance deux dés en même temps et que l’on additionne les deux nombres obtenus, on peut trouver n’importe quel nombre entre 2 et 12, mais tous ne sortirons pas à la même fréquence ; il suffit pour s’en convaincre de se rendre compte par exemple que le 2 ne peut être obtenu que d’une façon (1 sur chaque dé) alors que le 5, peut l’être de 4 façons différentes (1 et 4, 2 et 3, 3 et 2, 4 et 1).
• Autre cas de non équiprobabilité, dont nous pouvons parler avec assurance maintenant que le professeur von nous a tout expliqué : une tartine qui tombe d’une table n’a pas autant de chance de tomber du côté beurré que du côté sans beurre, à notre grand dam, il faut bien le dire.
• Last but not least, même dans le cas d’une partie de pile ou face, il n’est pas du tout évident dans la pratique que l’on ait équiprobabilité : si on lançait la pièce toujours exactement de la même façon, le résultat ne dépendrait que de la position de la pièce au moment du lancer (face ou pile en haut). Or on peut légitimement penser que celle-ci dépend du résultat obtenu la fois précédente : si je viens d’obtenir « face », je vais poser ma pièce avec « face » en haut, et donc augmenter mes chances d’obtenir l’un ou l’autre résultat au prochain lancer… Un magicien/physicien/mathématicien, Persi Diaconis, a fait des études poussées sur le sujet, et a obtenu, avec son protocole d’expérience, une fréquence de 51% pour le côté de la pièce qui était au dessus au moment du lancer. Un écart faible, mais significatif !…

Bon, mais nous sommes là pour parler des cas simples. À partir de maintenant, on va donc supposer qu’il y a bien exactement une chance sur deux d’obtenir respectivement pile ou face.

Ce qui justifie notre intuition d’équilibre à long terme entre le nombre de pile et le nombre de face, c’est la « loi des grands nombres ». Elle dit tout bêtement que si on répète un grand nombre de fois une expérience aléatoire, la fréquence d’apparition d’un évènement tend à se rapprocher toujours plus de la probabilité théorique d’apparition de cet événement. En gros, puisqu’il y a une chance sur deux que pile apparaisse, si on joue longtemps, la fréquence d’apparition de pile se rapprochera sans cesse de 50%. Ou encore : si je joue 1000 fois à pile ou face, j’obtiendrai approximativement 500 fois pile.

Attention encore! Cette fichue loi piège bien souvent notre raisonnement… Elle ne ne nous apprend en effet rien sur ce qui va sortir au prochain tirage : ce n’est pas parce qu’on a obtenu jusqu’ici plus de pile que de face que l’on a plus de chance d’obtenir face que pile la prochaine fois. Cette idée peut être perturbante quand on est en train de jouer plusieurs fois de suite, et que l’on trouve qu’il y a un trop gros déséquilibre en faveur de l’un ou l’autre. Mais elle est évidente si on se place du point de vue de la pièce, qui a priori n’a pas de cas de conscience, et nettement moins de mémoire qu’un poisson rouge (qui en a, lui, re-dixit le professeur von (un peu de fayotage ne nuit pas)), et qui donc n’a aucune raison de tenir compte du passé en ce qui concerne le prochain résultat. On parle d’« indépendance » des évènements : ils ne sont pas liés, tout est « remis à zéro » avant chaque lancer. C’est souvent le cas quand on parle de hasard : lancer de dé, loto… Mais beaucoup de personnes retiennent surtout la loi des grands nombres, et oublient ou comprennent mal ce qu’implique cette indépendance des évènements. Profitez-en pour vous amuser : si un jour vous voulez jouer au loto, par exemple, donc perdre, autant le faire avec panache et parier sur les numéros sortis au tirage précédent ! Tout le monde vous prendra pour un(e) original(e), et pourtant ces numéros ont bien sûr exactement la même chance de sortir que les autres ! (C’est d’ailleurs arrivé récemment en Bulgarie : http://www.20minutes.fr/monde/347973-Monde-Les-six-memes-numeros-sortent-deux-semaines-de-suite-au-loto-bulgare.php, et 18 personnes avaient justement parié sur les bons numéro la deuxième fois !)

Puisqu’on en est au loto : faites un tour sur internet pour trouver ce genre de page : http://www.lesbonsnumeros.com/loto/statistiques/numeros/nombre-sorties.htm sur lesquelles on trouve des statistiques très sérieuses de sorties de chaque numéro pour en déduire ceux qui « sont donc plus susceptibles de faire partie de la prochaine grille gagnante du Loto » (sic!) D’où la phrase bien connue : « le loto est un impôt sur les personnes qui ne connaissent pas les probabilités ».

Autre moyen de s’amuser, moins méchant et très pédagogique : improvisez vous magicien. Face à une personne non avertie, c’est très facile : demandez lui d’écrire une série de P et F « au hasard », au moins une vingtaine. Puis d’écrire une série de la même taille mais en jouant effectivement à pile ou face. Vous devriez rapidement repérer la série qui a réellement été tirée au hasard : celle qui aura le plus de « gros paquets » de pile ou de face qui se suivent, et/ou celle dans laquelle on trouvera le plus grand déséquilibre entre le nombre de pile et celui de face.

J’ai tenté l’expérience avec un collègue, qui a pourtant fait des études scientifiques, pour préparer ce dossier. Voici les deux séries (de 30) :

FFFPFFFPPFFPFFPFFFFFFPFPPPPPFF

et

PPPFFPFPFFPFPPPFFPFFFFFPPFFPPF

Vous avez un avis ?

C’est la deuxième qui a été fabriqué, ça saute aux yeux, même si le collègue s’est souvenu à la fin qu’il devait y avoir de gros paquets dans sa série, raison pour laquelle on trouve 5 F de suite ! Mais il l’a tout de suite « compensé » en mettant plus de P que de F par la suite. Résultat : 14 pile pour 16 face, un équilibre presque parfait.

Dans l’autre série, on trouve un paquet de 6 F, un de 5 P, peu de variations rapides type « PFPF », et 19 face pour 11 pile ! Jamais un être humain non déformé par des études de mathématiques n’aurait osé… Évidemment, les deux séries avaient exactement la même probabilité d’être obtenue. Mais il est beaucoup plus probable d’en obtenir une qui ressemble à la première qu’une qui ressemble à la deuxième.

Bref, imiter le hasard est franchement compliqué (Ce sujet est passionnant, mais ce dossier est déjà très long… on en reparlera) Tout ça parce que notre intuition a du mal à concilier « indépendance des évènements » et « loi des grands nombres ».

Encore une remarque importante : dire que plus on joue à pile ou face, plus la proportion de pile se rapproche de 50% ne dit pas que la différence entre le nombre de pile et celui de face est de plus en plus petite. Une petite illustration pour comprendre ça : fixons un point de départ, et représentons chaque « pile » par une montée d’un cran et chaque « face » par une descente d’un cran :

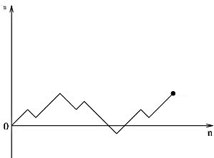
On obtient une « courbe » pointue, qui rappelle, si on prend une partie très longue, les fluctuations de la bourse :

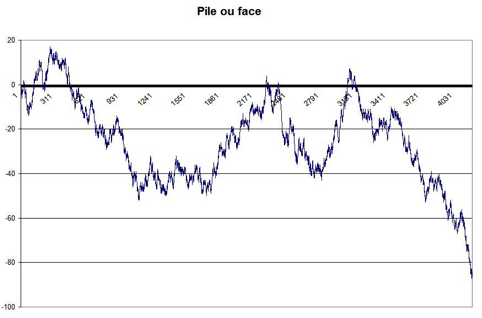
C’est ce qu’on appelle une « marche aléatoire de dimension 1 ».

La loi des grands nombres nous assure donc qu’à long terme, la courbe se rapprochera de la droite qui reste toujours au niveau 0, le départ de la « marche ». Sauf que non, c’est d’ailleurs assez visible dans l’exemple ci-dessus. Elle nous assure qu’en moyenne on s’en approchera. Ce qui veut dire que c’est l’écart à la droite divisé par le nombre de tirages qui s’en rapproche. En gros, ça ne marche que si on regarde cette courbe en s’éloignant sans cesse au fur et à mesure que le nombre de tirages augmente.

En revanche, si on regarde ce qui se passe en restant toujours à la même échelle, la courbe s’éloignera du point de départ : en moyenne, au bout de n tirages, elle est (ou est passée) à une distance de √n au dessus ou en dessous du point de départ. Bref, plus on joue longtemps, plus la courbe s’éloignera globalement de cette fameuse droite.

Et pourtant… Attention, ça fait mal, mais il faut le dire : la probabilité que cette courbe croise la droite du niveau 0 (autrement dit, qu’à un moment donné, il y ait eu exactement autant de piles que de faces de passés) au bout d’un temps fini est égale à 1. (Pour les non familiers des probabilités, on donne toujours la probabilité d’un événement sous la forme d’un nombre entre 0 et 1: 0, c’est impossible, 1, c’est certain).

Ce qu’affirme donc la théorie, c’est qu’il est certain qu’au cours de la partie, la courbe croisera cette droite. Or les esprits contestataires remarqueront avec justesse que c’est faux : il suffit d’imaginer la situation, très peu probable, certes, mais toujours possible, d’une partie qui serait constituée uniquement de pile, et d’aucune face. Puisqu’il existe au moins une courbe qui ne coupe pas la droite (et même bien plus, évidemment), comment peut-on affirmer qu’il est « certain » que ce sera le cas pour toutes les courbes ? Essayons d’expliquer tout cela calmement…

Imaginez par exemple que l’on cherche à prendre un nombre au hasard parmi tous les nombres, entiers ou non, que l’on trouve entre 0 et 10.

La probabilité que ce nombre se trouve entre 3 et 4 est de 1/10. Logique : le segment compris entre 3 et 4 est de longueur 1, alors que le segment sur lequel on pouvait choisir le nombre est de longueur 10. De la même façon, il y a 1 chance sur 5 pour que ce nombre soit entre 7 et 9. Mais comment répondre à la question : « quelle est la probabilité de tomber sur le nombre 5 ? » 5 n’est pas un segment, c’est un point. Il ne mesure rien, si c’est un segment, il est de longueur nulle. Pire qu’une aiguille au milieu d’une botte de foin !

La seule réponse cohérente, c’est de dire que cette probabilité vaut 0. Et pourtant, c’est évidemment possible de tomber sur 5 ! Les probabilistes disent dans ce cas que l’on trouve « presque sûrement » un nombre différent de 5. Cela signifie que cet événement est possible, mais que si on calcule la probabilité de l’obtenir, on obtient 0.

Voilà donc l’explication dans le cadre des parties de pile ou face : la courbe va « presque sûrement » recouper la droite horizontale, même s’il en existe qui ne la coupe pas… Perturbant, peut-être, mais cohérent, juré ! Mais évidemment, on pourrait imaginer que la partie a commencé au bout d’un certain nombre de coups. La courbe repassera donc par toutes les hauteurs par lesquelles elle est déjà passée. Et elle y repassera encore. Bref, si on laisse l’expérience se poursuivre à l’infini, cette courbe passera une infinité de fois par chaque hauteur !

Prenons maintenant du recul. Encore. Encore. Autant que possible. Les marches finissent par devenir invisibles. (c’est déjà un peu le cas avec les 4000 lancers!) Vous avez devant vos yeux (ou plutôt dans votre tête, puisque visuellement ce sera indiscernable du précédent dessin) un « mouvement brownien de dimension 1 ».

Et qui dit dimension 1 dit évidemment dimension 2 ! Allons-y…

Pour cela, plutôt qu’une partie de pile ou face parfaite, prenons un poivrot parfaitement imbibé, et parachutons-le en plein Manhattan. Dans cette ville, les rues et les avenues forment en effet un quadrillage quasi parfait. (Bon, en fait, on prendra un quadrillage parfait, et tant qu’à faire infini.)

Notre poivrot roule à terre à chaque carrefour, et est dans un tel état qu’il ne sait même plus par quelle rue il vient d’arriver. Il repart donc en choisissant de façon complètement aléatoire sa direction parmi les 4 choix possibles, jusqu’au prochain carrefour. Si vous voulez tenter l’expérience de façon plus sereine, il vous suffit d’une page de cahier quadrillé, et de deux pièces de monnaies différentes : vous avez alors 4 issues possibles (Pp, Pf, Fp, Ff), auxquelles vous n’avez plus qu’à associer une direction. En principe, vous obtenez un truc comme ça (à moins que vous n’ayez pas la patience de jouer 1000 fois!)

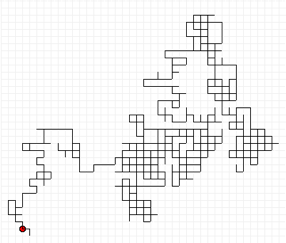
Pour cette « marche aléatoire de dimension 2 », ou « marche de l’ivrogne », on peut se poser les mêmes questions qu’en dimension 1, et les réponses sont les mêmes :

• Si on ne change pas d’échelle, on s’éloigne en moyenne d’une distance √n du point de départ au bout de n étapes.
• Si on divise cette distance par le nombre d’étapes, ce qui revient à « dézoomer » de façon proportionnelle au nombre de « pas », on se rapproche sans cesse du centre, donc en moyenne, les déplacements dans chacune des 4 directions ont tendance à s’équilibrer. (C’est d’ailleurs logique : à une distance moyenne de √n, cela signifie qu’après le changement d’échelle, la distance vaut environ √n/n, qui devient de plus en plus petite quand n grandit)
• La trajectoire repassera presque sûrement par le point de départ

Là encore, on peut imaginer s’éloigner tellement que le quadrillage disparaît. Le mouvement que l’on observe est alors le mouvement brownien de dimension 2, celui qui avait ce nom à l’origine. On pourrait aussi l’appeler la marche de l’ivrogne dans le désert : il n’y a plus de quadrillage, donc à chaque instant, la direction change aléatoirement pour prendre… n’importe quelle direction !

Ce mouvement brownien est au cœur de recherches contemporaines : il est l’un des sujets d’études de Wendelin Werner, qui a reçu pour cela la médaille Fields en 2006, et de Stanislas Smirnov, qui l’a reçu 4 ans plus tard (ils ont d’ailleurs travaillé ensemble !) C’est un objet fractal : contrairement aux marches aléatoires, d’aussi près qu’on le regarde, on ne verra que des virages, toujours. C’est le mouvement aléatoire parfait.

Sans entrer dans les détails de ce qu’ils ont fait… Wendelin Werner a, entre autre, réussi à préciser la description que l’on peut faire de l’ « enveloppe extérieure » d’un mouvement brownien. Stanislav Smirnov a beaucoup travaillé sur la modélisation de la percolation, ce phénomène de traversée d’un milieu plus ou moins poreux, comme l’eau à travers le café. La tâche faite par l’eau a une forme qui ressemble étrangement à cette enveloppe du mouvement brownien.

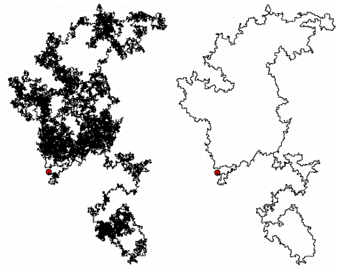
Ils ont également fait avancer des questions fondamentales, comme celle de connaître la probabilité que les trajectoires de deux pochtrons partant de deux points différents se croisent, par exemple… En dehors de l’aspect amusant de la question, elle peut intervenir dans les modélisations de réactions chimiques, par exemple, pour estimer le temps moyen de rencontre de deux molécules qui réagissent ensemble.

Passons maintenant à la 3D ! Notre poivrot peut maintenant en plus monter et descendre, avec la même probabilité dans chacune des 6 directions… (le pauvre, qu’est-ce qu’il s’est mis pour croire ça !)

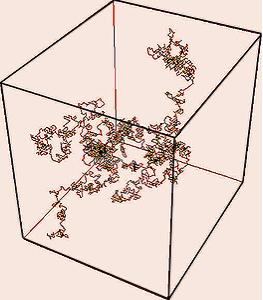
Incroyable mais vrai : il n’est plus du tout certain de repasser par son point de départ ! La probabilité est d’environ 1 chance sur 3 seulement ! Ce qui permet à l’auteur de cet article (http://images.math.cnrs.fr/Des-marches-aleatoires-pas-comme.html), d’où son tiré et des informations et des illustrations de ce dossier, de déconseiller fortement la perte d’un enfant dans un centre commercial, alors que dans la rue ce n’est pas si grave !

Et pour ceux qui aime rire, on peut bien sûr calculer cette probabilité en dimension plus grande, les résultats sont par exemple sur Wikipedia : http://fr.wikipedia.org/wiki/Marche_aléatoire au chapitre « théorème de Pὀlya ».

Pour finir, deux exemples d’application encore, pour ceux que ça intéressent : j’ai personnellement croisé un doctorant qui modélisait la trajectoire d’un virus jusqu’au noyau d’une cellule grâce entre autre au mouvement brownien.

Le mouvement brownien sans intersection (qu’il n’est d’ailleurs pas évident à modéliser semble-t-il) est apparemment utilisé dans la modélisation de polymères…

Pour tenter de s’approcher d’un mouvement brownien sans intersection, on peut encore une fois passer par les marches aléatoires. L’une des idées est alors d’« effacer les boucles » : dès que l’on croise le trajet, on « efface » la boucle que l’on vient donc de créer, et on repart du même point, comme si de rien n’était. Mais dès que l’on passe au mouvement brownien, tout se complique : au bout d’un temps même très court, il existe déjà une infinité de points sur lequel on est passé une infinité de fois…