Docteur Jeckyll…
En présentant le premier dossier, je me suis dit que j’avais quand même donné du hasard une vision assez négative. Le hasard contre intuitif, qui fait tout pour nous embrouiller, bourré de paradoxes… Cet aspect existe, bien sûr. Toutes les personnes qui ont passé un bac scientifique pourront le dire, les exercices de « proba » font partie des plus glissants. Et pourtant… face à ce versant « Mister Hyde », se trouve un versant bien plus positif du hasard. Grâce à lui, on peut notamment se sortir de problèmes inextricables…
L’idée de base est toujours la même : quand il y en a beaucoup ça va, c’est quand il y en a un seul qu’il y a des problèmes…
Revenons un tout petit peu sur la loi des grands nombres : en prenant l’exemple le plus simple, celle-ci dit par exemple que si on joue un grand nombre de fois à pile ou face, la proportion de pile sera d’autant plus proche de 50% que l’on joue longtemps. On peut le dire en termes plus précis : on sait calculer la probabilité que l’« erreur », l’écart à la fréquence attendue soit de plus de tant en fonction du nombre d’expériences. C’est cette certitude qui permet aux casinos (ou aux assurances) de pouvoir estimer combien ils vont gagner, en estimant simplement le nombre de joueurs (ou d’assurés). Pour résumer, donc, de l’accumulation de désordre jaillit l’ordre, pour peu qu’il y ait assez de monde. Autrement dit, dans un certain sens, on peut prédire le résultat, avec une certaine marge d’erreur que l’on peut évaluer.
Reprenons maintenant l’exemple dans lequel une partie consiste à jouer plusieurs fois de suite, par exemple 7 fois, à pile ou face. Le nombre de séries que l’on peut potentiellement obtenir est immense (27 pour être exact), et il est clair qu’on ne peut pas dire quelle série on va obtenir, ni même combien on aura obtenu de pile, et combien de face. Mais imaginons maintenant que nous sommes 100 à lancer 7 fois de suite chacun une pièce. Une fois de plus, le fait d’avoir un grand nombre d’expériences permet de prévoir dans les grandes lignes ce qui va se passer. Pour mieux le comprendre, remplaçons la partie de 7 pile ou face par un jeu qui lui est parfaitement équivalent : on fait tomber une bille sur un clou. Elle a une chance sur deux d’aller à gauche de celui-ci, une chance sur deux d’aller à droite. Jouer 7 fois de suite à pile ou face, c’est donc faire tomber une bille sur une planche à clou de 7 étages. Si elle arrive dans la case tout à gauche (A), c’est comme si on avait obtenu 7 fois de suite pile. Dans la case tout à droite (H), que des face. Dans la case juste un cran à droite de la première (B), cela signifie que l’on a obtenu exactement une fois face, et ainsi de suite… Cet objet célèbre s’appelle la « planche de Galton ».

Si on lance plein de billes, on peut prévoir la forme qu’aura le tas en bas : il y en aura en effet d’autant plus de billes dans une case que la probabilité de tomber dans cette case est élevée. Or la probabilité de tomber dans une case n’est pas la même suivant la case : il n’y a par exemple qu’un seul chemin qui mène à la case qui se trouve tout à gauche (une seule série ne comportant que des pile). Très peu de chances, donc, pour qu’une bille tombe dedans. Autrement dit, très peu de chances d’obtenir 7 fois de suite pile. Tomber dans la case juste à sa droite, cela signifie que l’on n’a obtenu que des virages à gauche, sauf une fois. Cette seule fois, ce seul virage à droite, peut se trouver à n’importe quel étage de la planche. Il y a donc autant de chemins qui mènent à cette case que d’étages à la planche, en l’occurrence, 7. Pour arriver dans la case qui se trouve encore un cran à droite, il existe encore plus de chemins, puisqu’il s’agit d’intercaler deux virages à gauches parmi 7 choix. Ils peuvent se trouver au début, à la fin, collés ou non, bref, il y a encore plus de façons de faire. Le plus grand nombre de chemins est pour les cases centrales : les billes qui arrivent dedans ont eu en gros autant de virages à gauche et à droite, et ça, il y a plein de façons de faire.
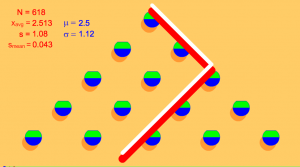
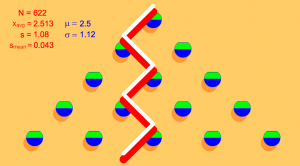 Fig 2 : Deux chemins différents aboutissant au même endroit… Et il y en a d’autres !
Fig 2 : Deux chemins différents aboutissant au même endroit… Et il y en a d’autres !On peut calculer plus précisément le nombre de chemins, et donc les probabilités de tomber dans telle ou telle case (donnons une piste : à chaque étage, une bille arrive sur un clou par la gauche ou par la droite. Il suffit donc d’ajouter le nombre de chemins qui arrivent sur les deux clous au dessus du clou en question pour savoir combien de chemins arrivent sur ce clou), mais ne nous compliquons pas la vie : on sait qu’en gros, il y aura plus de billes au milieu que sur les côtés. Et si on rajoute des étages, on estompe les différences entre les cases. À la limite, en imaginant un nombre d’étages infini et un nombre de billes infini, on se retrouve avec une courbe, et non plus des cases les unes à côté des autres. Cette courbe est essentielle en théorie des probabilité et ailleurs, c’est celle que l’on rencontre dès que l’on étudie une grande quantité de données, que ce soit à propos de plantes, d’ornithorynques ou de pluviométrie : la courbe de Gauss.
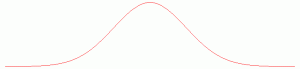
Prenons l’exemple de la taille de la population française : a priori, tout le monde se rangera autour d’une taille moyenne, avec beaucoup de monde à proximité de cette taille, et quelques uns très grands ou très petits. Si on cherche une description plus précise, la courbe de Gauss donne en principe une bonne approximation. Bon, il faut savoir autour de quelle valeur elle est centrée, et si elle est plutôt pointue ou étalée, mais l’équation générale sera toujours la même.
Cela peut semble surprenant, c’est en fait assez naturel : il suffit de s’imaginer que nous sommes dans une case en bas d’une très grande planche de Galton, et nos ancêtres des clous de cette planche ; à chaque génération, des gênes se sont mélangés, et nous avions une chance sur deux de recevoir tel ou tel héritage. Il se rajoute à ça les conditions de vie, d’autres facteurs, mais dès qu’ils sont suffisamment « mélangés » et nombreux, ceux-ci vont également donner une répartition « en cloche » de la population. Nous sommes donc issus d’un mélange d’immenses parties de pile ou face. Pas étonnant de retrouver des lois de Gauss pour bien des caractéristiques.
Bref, quand on observe quelque part la loi de Gauss, autrement appelée « loi normale », c’est qu’il n’y a rien de spécial à expliquer. Dans le cas contraire, bien sûr, que ce soit en biologie, en physique, en économie ou autre, c’est qu’au contraire, il y a une explication à trouver.
Ce fut d’ailleurs le cas lors d’une sombre affaire d’élections douteuse en Russie il y a un peu plus d’un an (http://images.math.cnrs.fr/Za-normal-noe-raspredelenie.html), où la connaissance de cette fameuse loi de Gauss a permis à des manifestants de prouver
– qu’ils s’y connaissaient en maths
– qu’ils avaient de l’humour
– que le parti de Poutine avait procédé à un bourrage d’urne…
– que les gens ayant procédé à ce bourrage ne devait pas se douter qu’il est compliqué d’imiter le hasard
Bref, pour conclure sur ce thème : si plutôt que d’essayer de connaître quelque chose de précis, individu par individu, on cherche plutôt une photo globale, c’est souvent bien plus simple. Cette idée peut s’appliquer dans deux nombreuses situations, et notamment quand il s’agit de modéliser un phénomène complexe…
Mettez vous par exemple deux secondes à la place d’un physicien qui veut modéliser le déplacement d’une molécule d’eau dans un verre. Impossible a priori de savoir exactement où elle va aller. On peut bien essayer de savoir dans quelle direction elle va, à quelle vitesse. Mais dès qu’elle rencontre une autre molécule, elle va se cogner, et changer de direction. Et ça va arriver très souvent, et sa position va changer la trajectoire des autres molécules, qui vont elles même interagir… Bref, impossible en pratique de déterminer effectivement quelle va être la trajectoire précise d’une molécule.
Deuxième expérience traumatisante : essayez de vous mettre à la place d’une personne chargée de modéliser le réseau téléphonique d’une ville. Partout, des commutateurs, des antennes, se renvoient des signaux, à tout instant, un signal cherche quel chemin suivre pour se rendre jusqu’au téléphone de votre interlocuteur. La question n’est pas de trouver le chemin le plus adapté à un moment donné, mais de tenter d’estimer le coût de l’installation, de voir si le réseau est correct, fiable, combien il coûte en installation, en entretien, sachant combien il y a de commutateurs, d’antennes, tout ça.
N’essayez surtout pas de résoudre ces problèmes pour de vrai, c’est impossible en pratique, même avec le plus performant des ordinateurs. D’autant qu’il existe une méthode bien plus simple : faites comme si tout cela se faisait parfaitement au hasard. Ce ne sera pas trop faux, vu la complexité des problèmes, et au moins vous pourrez dire quelque chose, faire une modélisation calculable, de taille raisonnable… Pour les commutateurs, donc, on « lance » des points aléatoirement sur un plan, et on les relie de façon pas tout à fait aléatoire, mais pas loin. Ça y est, vous avez votre modèle. Pour les molécules d’eau, faites comme si chacune d’entre elles se déplaçait en suivant un mouvement brownien (cf premier dossier sur le hasard). Sauf si un courant particulier existe, cette façon de simplifier sera valable. Et contrairement aux apparences, ça simplifie tout !
Parfois, il faut tout de même améliorer un peu ce genre de modèles, on ne peut pas se contenter d’un hasard pur, comme par exemple s’il existe un courant dans l’eau. Mais il est toujours possible de « pondérer » le hasard, c’est à dire de ne pas donner la même probabilité à toutes les directions possibles, par exemple.
Encore mieux : il peut être bon parfois d’introduire délibérément du hasard là où on en n’attendrait pas pour résoudre un problème insoluble ou presque.
Vous voulez par exemple calculer la surface d’une forme donnée. Si on a une information sur cette surface, comme l’équation ou une description géométrique du bord, on peut chercher à faire un calcul exact. Mais c’est rare… Si vous ne savez rien, et que vous acceptez de n’avoir qu’une réponse approximative, c’est facile : inscrivez-la dans un carré, et lancez des grains de riz aléatoirement dessus. Certains vont tomber sur la surface, d’autre à côté. La loi des grands nombres nous dit que pour un grand nombre de grains de riz, la proportion de grains sur la forme est proportionnelle à la surface de cette forme. Dit autrement : nombre de grains de riz sur la forme/ nombre de grain de riz total = surface de la forme/surface du carré. Enfin à peu près, bien sûr, mais plus on lance un grand nombre de grains, plus l’erreur est petite.

Vous pouvez éprouver cette méthode en calculant la surface d’un disque. C’est long, pour avoir un résultat acceptable, il faut lancer beaucoup beaucoup de grains de riz, mais ça marche !
La célèbre méthode de Buffon utilise d’une autre manière le hasard pour calculer une valeur de pi, en lançant des aiguilles sur un parquet. En fonction du nombre d’aiguilles qui sont à cheval sur deux lattes, on peut effectivement calculer la fameuse constante, mais là encore… en théorie ! (pour quelques explications, et une application qui montre qu’effectivement ça marche, mais qu’effectivement c’est très très long : http://therese.eveilleau.pagesperso-orange.fr/pages/truc_mat/textes/buffon.htm)
Le voyageur de commerce est un autre problème bien connu : celui-ci doit se rendre dans un certain nombre de villes, puis rentrer chez lui. Évidemment, son objectif est de trouver l’itinéraire le plus court possible.
A priori, on ne sait pas mieux faire, ou presque, pour résoudre ce problème de façon parfaite, qu’en essayant tous les chemins possibles, en calculant à chaque fois leur longueur et en les comparant. C’est beaucoup trop long dès que l’on a un nombre un peu trop important de villes, même pour un ordinateur.
On sait pourtant trouver une réponse raisonnable dans un temps raisonnable, grâce à plusieurs méthodes. L’une d’elle, particulièrement belle je trouve, se sert du hasard : prenez des « fourmis virtuelles », qui laissent des phéromones derrières elles, autrement dit augment un certain nombre associé aux routes qu’elles ont empruntées. Elles parcourent toutes les arêtes du graphes formé par tous les chemins qui relient les villes entre elles. Dans l’algorithme, elles ne vont pas complètement au hasard : elles ont une probabilité plus forte de suivre un chemin qui a beaucoup de « phéromone » virtuelle. Petit à petit, comme un chemin plus court est parcouru plus vite, il va « sentir » plus fort, donc être plus suivi, et donc éliminer petit à petit tous les autres chemins. Bon, encore une fois, pas sûr qu’elles tombent sur LE chemin le plus court, mais ce sera un chemin de taille « raisonnable ». Et on peut le calculer en un temps raisonnable. Une application là http://interstices.info/jcms/c_7083/lintelligence-en-essaim-ou-comment-faire-complexe-avec-du-simple?part=2, avec des explications, mais ça va trop vite à mon goût !)
Encore une utilisation, et non des moindre : le hasard peut être utilisé pour coder des messages ; communications sur internet, données bancaires, militaires…
Mais il y a un petit problème : c’est très bien, c’est très beau, le hasard peut servir dans bien des situations à se sortir d’affaire. Mais pour tout ça, il faut avoir une série de nombres (ou de directions, ou autres, mais disons de nombres, pour un ordinateur ça se réduit finalement toujours à ça…) « au hasard ».
Et ça, on a vu aussi la dernière fois que ce n’était pas facile : ne serait-ce que simuler une série de pile ou face « au hasard » est compliquée pour un être humain. Et un ordinateur ? Il ne fait que ce qu’on lui demande… Comment lui demander de fabriquer du hasard ?
Plusieurs méthodes ont été proposées, Mais beaucoup sont loin d’être parfaites.
L’une des plus anciennes, est celle de von Neumann : on prend un nombre, mettons de 4 chiffres. On le multiplie par lui même. On obtient un nombre, a priori de 8 chiffres. On récupère les 4 chiffres du milieu, et on recommence… Très difficile a priori d’imaginer un lien logique évident entre deux nombres consécutifs de cette suite. Sauf qu’il suffit d’essayer avec quelques nombres pris au hasard pour se rendre compte d’une grande faiblesse de ce genre de systèmes : pour beaucoup de nombres de départs, on va « boucler » très vite (repasser par un nombre déjà obtenu, donc obtenir toujours la même série), ou pire faire du sur place (par exemple à partir du moment où on a un 0 en première position, on se rapproche de 0000, et on y reste!)
Autre tentative : le calcul modulaire, c’est à dire celui que l’on fait quand on est capable de dire, à 14H, qu’il est 2H. En gros, on considère qu’une fois revenu à un certain nombre (ici 12, mais ça peut être autre chose), on revient à 0. On dit que l’on calcule « modulo 12 ». Disons maintenant que je choisis un nombre pour commencer, puis que pour trouver le suivant, je le multiplie 27 fois par lui même modulo 2337, et ainsi de suite. Si on prend quelques précautions sur les nombres choisis, on peut ainsi obtenir une imitation pas si mauvaise du hasard…
Mais là encore, le risque de boucle courte ou de point stable est grand…
Autre idée toute bête d’un autre ordre : se servir dune « banque de donnée » déjà constituée, comme les décimales de pi par exemple. On n’a en effet jamais trouvé de logique dans cette suite de chiffres. On sait juste que :
– Il y en a une infinité
– Il n’y aura jamais de période…
De plus, il semblerait (ce n’est qu’une conjecture vérifiée jusque là par toutes les décimales connues) que ce nombre soit « normal ». Définition pour ceux qui ont raté l’allusion à cette propriété dans le dossier de Nico sur pi : un nombre normal est un nombre dans lequel on trouve à la même fréquence chaque chiffre, mais aussi chaque paquet de deux chiffres, et bien sûr chaque paquet de trois, quatre, cinq… chiffres. Exactement ce que l’on peut raisonnablement attendre d’une série de chiffres obtenue en tirant au hasard ! Bon, ça ne suffit pas. Prenez le nombre de Champernowne, par exemple : 0,1234567891011121314151617181920… Il est bien sûr normal, mais on ne peut pas dire que les chiffres arrivent dans un ordre inattendu. Mais pour pi, personne n’a encore trouvé de logique dans l’ordre d’arrivée des décimales, ni d’ailleurs ne voit pourquoi ce serait le cas ; il ne paraît donc pas aberrant de prendre la suite de ses décimales comme approximation du hasard, on en connaît plusieurs dizaines de milliards ! Évidemment, pour une méthode de Monte Carlo, et surtout pas pour coder un message : cette suite est légèrement connue de tous…
Mais les véritables idées efficaces pour qu’un ordinateur crée du hasard, c’est celles qui se servent du fait que les ordinateurs eux-mêmes ne sont pas parfaits. Par exemple, ils ne mettent jamais exactement le même temps à effectuer une opération. Or les horloges qui se trouvent dans nos ordinateurs sont en général très précises (de l’ordre du centième de seconde au moins, même de la milliseconde). Si vous prenez régulièrement la milliseconde de l’instant où vous avez besoin d’un nombre aléatoire, par exemple, et que pour plus de sécurité vous lui faites subir une transformation via un calcul bien choisi, ça a de bonnes chances de ressembler à du hasard. L’idée de collecter de telles valeurs liées au fonctionnement de l’ordinateur est utilisée dans des systèmes de cryptage tout ce qu’il y a de plus sérieux. Comme quoi, les bouts de ficelle ont de l’avenir !…
Pour finir, une petite réapparition de Mr Hyde, deux petites histoires qui n’avaient pas lieu d’être dans la première partie ni dans cette deuxième partie, mais que je trouve assez jolies et troublantes pour les citer :
- Le paradoxe de Monty Hall. Un grand classique !
À une émission de télévision, le gagnant se trouve pour finir face à trois portes. Derrière deux d’entre elles, une chèvre. Derrière la troisième, une voiture. Évidemment, le principe est que l’on gagne ce qui se trouve derrière la porte choisie. Or, une fois le choix du spectateur fait, le présentateur, histoire de faire monter la tension, ouvre l’une des deux portes non choisie, derrière laquelle se trouve une chèvre (on suppose, fait important, que lui sait où se trouve la voiture, et qu’il n’ouvre pas la porte derrière laquelle celle-ci se trouve). Il demande ensuite au malheureux vainqueur s’il veut changer son choix ou non. La logique nous hurle, quand on n’a jamais entendu parler de cette histoire, que ça ne change rien… Et pourtant…
Voici une façon de répondre, condensée : Le spectateur a une chance sur trois de choisir du premier coup la voiture. Dans ce cas, le présentateur ouvre une des deux portes restantes au hasard, et changer de porte fait perdre le spectateur.
Le spectateur a deux chances sur trois de choisir une chèvre pour commencer. Dans ce cas, le présentateur n’a pas le choix de la porte à ouvrir pour montrer une chèvre, et en changeant, le spectateur gagne.
On multiplie donc ses chances de gagner par deux en changeant de choix…
- Autre histoire du même tonneau : vous vous rendez chez des gens que vous connaissez peu. Vous savez qu’ils ont 2 enfants, dont une fille. Quelle est la probabilité pour que l’autre soit un garçon ?
Et non, pas une chance sur 2 : il y a trois types de familles possible avec au moins une fille : Fille/Garçon, Garçon/Fille, et Fille/Fille. Dans deux cas, l’autre enfant est un garçon, il y a donc deux chances sur trois pour que le deuxième soit un garçon.
En revanche, si on sait que l’aînée est une fille, il y a bien une chance sur deux pour que le deuxième soit un garçon…
Pour aller plus loin…
- Vidéo “30 minutes pour comprendre” de l’Université de Rouen: “La géométrie, le hasard et le téléphone”



