Qu’est ce qu’un cristal ? Des fois que vous ne l’ayez déjà fait, regardez un grain de sel de près. (du gros sel, c’est mieux)

On voit des cubes. Et oui. Bon, pas que, d’accord, mais on en voit. Et on se dit que quand même, ce n’est pas du hasard. Surtout que dans certains cas, c’est presque tous, de beaux cubes.

Et d’autres cristaux que l’on trouve dans la nature ont des formes tout aussi étonnantes de régularité, qui conservent cette régularité si on les casse. L’idée qui peut venir naturellement est donc que ces matériaux sont constitués de petites briques élémentaires toutes identiques et très bien rangées. Leur forme est soit la même que ce que l’on observe en grand, soit une forme qui permet de l’obtenir. Un exemple simple : si le cristal a une forme de cube, on se dit qu’il y a des angles de 90° quelque part à petite échelle. Alors que s’il a la forme de prisme hexagonal, comme la chaussée des géants, il paraîtrait tordu d’imaginer des petites briques en forme de cube…

Pour ceux qui ont besoin d’images plus proche de leur réalité : imaginez une tablette de chocolat géante. Si vous la cassez, les brisures formeront toujours des angles droits entre elles (à part si vous prenez des tablette trop fines, mais ne compliquons pas, s’il vous plaît). À l’inverse, si vous imaginez un fabriquant de chocolat au miel qui pour des raisons marketing vend des tablettes où les carreaux de chocolat sont en forme d’hexagones, les angles formés au bord de la tablette (qui ne seront pas rectilignes) ne pourront être (vus de loin) que de 60° ou 120°.

En première approche, je vais donc définir les cristaux comme (Attention, éloignez les chimistes pour cette introduction de cristallo pour les nuls. Non que je ne dise des conneries (encore que), mais parce que je vais tellement simplifier à outrance que leurs oreilles risquent de saigner…)

Donc une première définition des cristaux pour les matheux ou pour les nuls, c’est pareil : des petits machins tous identiques vont se ranger de façon régulière. Et je me fous complètement de savoir si ces machins sont des atomes, des molécules ou autres ions, s’il y a plusieurs sorte ou une seule… Vous pouvez rappeler les chimistes.

L’idée est donc, pour étudier les cristaux et les classer, de s’intéresser à leurs « symétries », c’est à dire à ce qui est conservé à toutes les échelles, ce qui concerne notamment ces histoires d’angles.

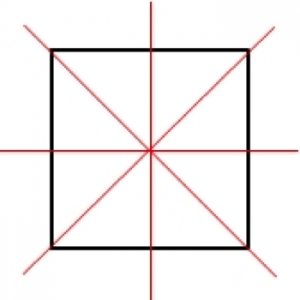
Une symétrie, pour un scientifique, est quelque chose de beaucoup plus large que la simple symétrie axiale que l’on apprend à l’école. Celle-ci est une symétrie car si l’on retourne la figure suivant cet axe, on observe exactement la même chose qu’avant ce retournement. Une symétrie est en fait ce type de régularité : un mouvement qui est tel qu’après l’avoir fait, l’objet auquel on s’intéresse est dans la même position qu’avant d’avoir bougé.

Un carré a donc 4 axes de symétrie, (vertical, horizontal, et les deux diagonales), mais a également un « centre de symétrie d’ordre 4 » : si vous le faites tourner d’un quart de tour autour de son centre, il sera dans la même position qu’avant ce mouvement.

Bien entendu, au centre d’un triangle équilatéral, il y a un centre de symétrie d’ordre 3, au centre d’un pentagone régulier un centre de symétrie d’ordre 5, et ainsi de suite…

Mais le but est de se placer au centre d’un « cristal », c’est à dire d’un motif qui se répète.

Un mathématicien normalement constitué qui entend parler de cristaux pense immédiatement aux pavages périodiques. Périodique, cela signifie qu’un petit morceau bien choisi permet de reconstituer l’ensemble du pavage. C’est notamment ce qui se passe sur un papier peint, ou sur un carrelage.

Prenons donc (c’est l’exemple le plus simple), un pavage fait de carré. Le carrelage de votre salle de bain fera très bien l’affaire, pourvu que vous l’imaginiez infini (allez, quoi, un petit effort !) Où que vous soyez en ce moment, vous avez forcément pas loin de vous un pavage fait de carrés. (cahier, plafond, carrelage…) Regardez le bien en face. Au centre de n’importe quel carré, il y a un centre de symétrie d’ordre 4 : je vous rappelle que cela signifie qu’un quart de tour autour de ce point remet le pavage exactement dans la même position. Mais au sommet de chaque carré, il y a également des centres de symétrie d’ordre 4. Et au milieu de chaque côté, il y a des centre de symétrie d’ordre 2, c’est à dire que des demi-tours le laisseront inchangés.

Attention, concentration : le carrelage formé d’octogones et de carrés.

Celui formé d’hexagones réguliers.

Puisque nous sommes à la radio, j’ai prévu des petits exemples audio. Petite pause, qui permettra je l’espère à ceux qui se noient de raccrocher aux wagons.

Un motif périodique, c’est un motif qui se répète, comme celui ci par exemple.

Mais ici, il n’y a visiblement aucune régularité, aucune symétrie autre que le fait de se répéter.

Alors que dans ce motif, on entend clairement une symétrie : il peut être écouté à l’endroit ou à l’envers sans que cela ne change rien. (c’est un palindrome). Du coup, quand on le répète, la « mélodie » obtenue possède également cette symétrie. Et on peut « retourner » cette mélodie autour de la note centrale du motif ou entre deux motifs successifs.

Même chose dans ce deuxième motif, pourtant très différent : ces deux « mélodies » ont les mêmes symétries.

Cet autre motif a une symétrie très différente : on peut inverser les graves et les aigus, cela donnera la même chose.

C’est à peu près tout ce qu’on peut imaginer comme symétries pour une telle mélodie, ce qui est bien pauvre, il faut le reconnaître. À part une mélodie qui cumule les deux symétries déjà entendues :

J’espère au moins que ces exemples vous ont permis de comprendre l’idée de périodicité, et l’idée des motifs qui ont une même symétrie sans être identiques.

Reprenons. Un pavage peut donc avoir toutes sortes de symétries ; Sauf qu’il ne peut pas en avoir tant que ça. En fait, de même que le pavage formé d’octogones et de carrés n’est qu’un pavage de carrés décoré, tout pavage périodique est une décoration ou une version étirée du pavage de carrés ou de celui d’hexagones réguliers. Il suffit de tenter de créer des pavages périodiques, d’en observer pour s’en convaincre. Un dernier petit effort d’imagination pour tenter de comprendre un peu pourquoi : intéressons nous aux pavages réalisés uniquement avec des polygones réguliers, dont tous les côtés sont les mêmes et tous les angles également. Il est très simple et très rapide de les trouver tous :

Avec des triangles équilatéraux, on peut évidemment paver : il suffit d’en placer 6 pour former un hexagone régulier, et vogue la galère.

Avec des carrés… bon, on dit que c’est fait.

Avec des pentagones réguliers… Il faut remarquer que plus un polygone régulier a de côtés, plus ses angles sont grands. Or dans le pavage réalisé avec des carrés, ceux ci se trouvent par 4 autour de chaque sommet ; dit autrement, l’angle d’un carré est un quart de tour complet. Et nous savons aussi que 3 angles d’hexagones permettent de faire un tour complet. Pour paver avec des pentagones réguliers, il faudrait donc pouvoir en mettre entre 3 et 4 autour de chaque sommet… C’est impossible ! Et c’est bien ce que l’on observe : quand on commence à tenter le pavage, on en place 3, et il reste un angle vide, trop petit pour placer un 4ème…

Au dessus de l’hexagone, c’est donc aussi impossible : il est impossible de ne placer que deux polygones autour d’un sommet. Il n’y a donc pas d’autres pavage régulier.

Dans ces pavages, on trouve des symétries d’ordre 2, 3, 4, et 6. Et rien d’autre. Et tout pavage, découlant de lui, peut avoir ces symétries, éventuellement moins (pensez à ce qui se passe si on transforme les carrés en rectangles : les centres de symétrie ne sont plus que d’ordre 2), mais pas plus, pas d’autres.

La cause est donc entendue, il ne peut y avoir, dans les pavages périodiques, que des symétries d’ordre 2, 3, 4, et 6.

J’entends ça et là quelque raclements de gorge, de gens qui s’impatientent, qui pensaient entendre parler de cristallo et n’entendent que des maths depuis un moment… Votre patience va être récompensée, nous sommes ici en plein cœur de la cristallo ! Ce résultat essentiel permet en effet, en faisant la même étude en 3D, de prévoir, de lister, de classer toutes les formes qu’un cristal peut prendre ! D’ailleurs, une grande partie de l’étude des pavages périodiques a été menée par un chimiste, Fedorov.

On peut donc faire la liste de tous les pavages (et donc des types de cristaux) possibles à partir de toutes les symétries qui peuvent cohabiter. Il existe 17 types de pavages à plat. Et dans les deux cas, outre les axes ou plans de symétries, il n’existe que des symétries d’ordre 2, 3, 4, et 6.

Plongeons maintenant du côté chimiste de l’affaire. Depuis le début du 20ème siècle, ces derniers possèdent un test extraordaire pour étudier la matière : les rayons x.

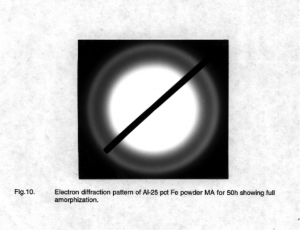
Ils bombardent la matière à étudier avec, et les rayons x la traversent. Dès lors, de deux choses l’une : soit les rayons x qui ressortent forment une tâche informe, ce qui signifie que la matière n’a aucun arrangement particulier, elle est en désordre, on appelle ça de la matière « amorphe ».

Là, ça ne ressemble à rien.

Soit ce qui ressort est un réseau de points lumineux bien rangés, qui possède les même symétries que le cristal traversé.

Là, ça a traversé du cristal, avec des symétries d’ordre 4, de toute évidence.

Que du bonheur. La cristallographie peut commencer, le test est simple, efficace, nous donne tout de suite des informations sur la façon dont le cristal est rangé, parfait.

La définition des cristaux date de cette époque en substance : matière dont le spectre de diffraction est périodique.

Et donc tous les chimistes connaissent la “restriction cristallographique” qui liste toutes les symétries que l’on peut trouver dans un cristal.

En 1982, Daniel Schechtmann étudie un nouveau matériau, un mélange d’aluminum et de manganèse refroidit rapidement. Premier réflexe, rayons x. Et là… Bim, des petits points tout bien rangés, nickel, il s’agit d’un cristal ; sauf que les points sont rangés en très jolis… pentagones réguliers ! Des symétries d’ordre 5 dans un cristal ? Impossible, Schechtmann le sait bien, il l’enseigne à ses étudiants de première année, et sait même faire la démonstration bourré en faisant le poirier !

Perturbé, il va en parler à son chef, qui lui dit gentiment de réviser ses cours et de ne plus l’embêter pour des conneries. Il insiste, veut publier, se fait jeter… Et même virer de son labo, tente d’écrire à des chercheurs un peu partout dans le monde…

En 1984 enfin, il arrive à se faire publier. Et d’autres cristallographes l’ont rejoints. Et enfin, les matheux entendent parler de ses malheurs. Et lui disent : « bah ? Il est où le problème ? C’est du pavage quasi périodique, on a trouvé ça il y a 10 ans ! »

Bon, j’embellis sûrement un peu, mais c’est l’idée.

Retour donc dans les années 70 et même en 61, avec le problème de Wang. Les matheux se posent une question de fin de soirée bien comme on les aime : « et les gars, est ce que ce serait possible de faire un pavage pas périodique ?

• Ben ouais, tu prends que des pièces différentes, une infinité, comme ça t’es tranquille
• Ah non, c’est de la triche, avec un nombre fini de pièces seulement, cap ou pas cap ? Hein ? »

Évidemment, cette reconstitution n’engage que moi et doit être assez loin de la réalité. Quoique.

Le but est donc, de trouver un nombre fini de pièces différentes (on a autant de pièces qu’on veut, mais le nombre de formes différentes est fini) qui permettent de ne réaliser qu’un pavage qui N’EST PAS périodique, c’est à dire tel qu’aucun extrait, aussi grand qu’il soit, ne permette de le reconstituer en le répétant bêtement.

Voilà la meilleure illustration musicale que j’ai pu trouver de l’idée : les décimales de pi au piano (pour les amateurs, pi est d’abord traduit en base 12, vu qu’il y a 12 notes différentes).

On sait, c’est démontré depuis bien longtemps, qu’il n’y a en effet aucune période dans les décimales de pi, c’est à dire aucun paquet de chiffre qui permet d’obtenir toutes les décimales en se contentant de les répéter. On ne dispose pourtant que de 12 notes, mais on peut faire une mélodie non périodique. Attention, cela ne signifie pas que l’on n’entendra plus jamais telle ou telle série de notes, ça au contraire on est sûr qu’on l’entendra si on attend assez longtemps, mais qu’il n’existe aucun extrait permettant de la recréer intégralement, ça change toujours.

Plusieurs mathématiciens ont trouvé des solutions à ce problème de pavage non périodique. Le plus connu est sans aucun doute le pavage de Penrose, trouvé dans les années 70, qui n’utilise que deux formes différentes ! Et dans ce pavage, partout, partout, partout… des étoiles à 5 branches !

Un bon gros extrait du pavage de Penrose.

Donc des symétries d’ordre 5, mais qui ne s’appliquent à chaque fois que sur des extraits plus ou moins grand du pavage, pas sur l’ensemble.

Ces pavages ont permis assez rapidement de trouver de bons modèles pour ces cristaux impossibles, observés par d’autres que Schechtmann après sa publication. Et en…92 (oui, la science n’avance pas toujours très vite), l’union des cristallographes changeait enfin la définition des cristaux pour y inclure les quasi cristaux. Entre autres causes, cette lenteur vient de l’opposition de Linus Pauling, double prix Nobel (Paix et chimie), qui ne voulait pas entendre parler de ces trucs. Mais la morale est sauve, puisqu’en 2011, Schechtmann a reçu le Nobel à son tour pour sa découverte…

Il reste, si j’ai bien compris, un mystère à éclaircir : même en prenant les bonnes formes, un pavage quasi périodique n’est pas évident du tout à réaliser : il arrive que même en suivant scrupuleusement les contraintes, on soit obligé de démonter une partie de ce qui est fait pour recommencer autrement. Comment donc expliquer que de telles structures puisssent malgré tout apparaître de façon stable dans la nature ??