Dossier de l’épisode #102.

On connaît les nombres premiers depuis si longtemps qu’on ne sait pas exactement depuis quand. Mais pourquoi donc les distinguer ? Qu’ont-ils de si essentiel ?

L’expérience toute bête des « nombres figurés » permet très rapidement de saisir leur importance. Les nombres figurés sont un domaine de recherche qui lie arithmétique et géométrie. Qui liait devrait on dire, je n’ai pas entendu parler de recherche de ce côté là depuis l’Antiquité…

Il s’agissait de dessiner des figures géométriques régulières, harmonieuses, à l’aide de cailloux. Le nombre de cailloux utilisés était donc un nombre qui avait comme propriété d’être de cette forme. Par exemple, 3, 6, 10 sont des nombres triangulaires, car on peut dessiner un triangle équilatéral avec ce nombre de cailloux :

Il en existe une infinité, bien sûr. Et il est facile de trouver le suivant dans la liste : tous ces nombres sont de la forme : 1 + 2 + 3 + 4 +… + n. Le 3^è nombre triangulaire est donc 6, le suivant 6 + 4, puis 10 + 5, et ainsi de suite. Mieux, on peut calculer directement combien vaut le énième nombre triangulaire sans avoir à calculer les précédents, autrement dit effectuer la somme ci dessus directement. Comment faire ? Plusieurs démonstrations existent, mais la plus simple et la plus belle est sans doute celle qui passe justement par les nombres figurés : prenez votre triangle, et alignez toutes les lignes à gauche (en rouge) (pour les utilisateurs habituels de logiciels d’écriture, on passe d’un « centré » à un « aligné à gauche », mais le contenu des lignes reste le même).

Recopiez maintenant ce triangle « tête bêche » avec le premier (en bleu). Vous avez exactement deux fois trop de cailloux. Mais il est facile de compter combien il y en a en tout : n lignes (ici 8 lignes), (n + 1) colonnes (ici 9), il y a donc n x (n+1) cailloux (8 x 9), et comme il y en a deux fois trop, on divise ce résultat par deux (ici 8 x 9/2 = 36, le 8^è nombre triangulaire est donc 36). Et hop ! Pour savoir directement quel est le 42^è nombre triangulaire donc, pas d’angoisse : il vaut 42 x 43 / 2, soit 903. Ces nombres triangulaires n’ont plus de secret pour nous, donc plus d’intérêt.

Même chose pour les nombres carrés : on peut évidemment calculer très facilement le n^è nombre carré : il suffit de multiplier ce nombre par lui même. Moins connu mais tout aussi simple, le moyen de passer d’un nombre carré au suivant, qui se trouve très facilement en passant encore une fois par les nombres figurés, les curieux apprécieront.

Les figures ne manquent pas : pyramide, cube, pentagone… Mais le classement qui a eu de l’importance pour la suite est celui fait en nombre composés et nombres premiers. Là encore, il s’agit de géométrie : quels sont les nombres qui sont composés à partir d’autres nombres, c’est-à-dire que l’on peut construire à partir d’autres ? On peut aussi les appeler nombres « rectangles », dans lesquels rentrent bien évidemment les nombres carrés. Quatre cailloux, par exemple, peuvent être disposés en un carré de deux sur deux.

Le nombre 4 est donc en quelque sorte fabriqué à partir de 2. De même, 6 peut être représenté sous la forme d’un rectangle de 2 lignes de 3 cailloux, 15 comme un rectangle de 3 sur 5, et ainsi de suite. Bien sûr, pour certains nombres, comme 12, il y a plusieurs solutions. Mais pour certains, c’est impossible : ce sont les nombres « premiers ». Attention, pas d’oubli, 2 en fait donc bien partie ! C’est le seul nombre pair qui fasse partie des nombres premiers, bien sûr, puisque tous les autres peuvent par définition être rangés sur deux lignes de même taille. Et 1 pose un problème, puisqu’évidemment, on peut toujours mettre n’importe quel nombre sur une ligne. Peut-on dire pour autant qu’on « fabrique » ce nombre avec 1 ? Ce n’est pas très intéressant. Il vaut donc mieux l’exclure de la liste, on verra par la suite qu’il y a plusieurs situations qui sont ainsi rendues plus « confortables ». Plutôt que la définition habituelle, je préfère dire que les nombres premiers sont donc ceux qui ne peuvent pas être divisés. Étant entendu que diviser par 1 ou par soi-même n’a aucun intérêt, et peut difficilement être appelé « diviser ».

Ces nombres sont donc ceux qui sont à la base, qui ne peuvent pas être construits à partir d’autres, les « briques élémentaires ». Sans être très chimiste, la comparaison avec les éléments de base que l’on trouve dans le tableau périodique des éléments me parle : n’importe quelle molécule est un assemblage de ces atomes, qui eux ne sont pas réductibles (enfin sauf si on commence à regarder ce qu’il se passe à plus petite échelle, bien sûr…). Autre comparaison qui vient naturellement : les couleurs « primaires », qui sont nécessaires (s’il en manque une, on ne s’en sort pas) et suffisantes (il n’en manquera pas) à créer toutes les autres couleurs. Bref, cette idée de trouver les éléments de base qui permettent de reconstituer tout un univers n’est pas propre aux mathématiques (ni d’ailleurs à la théorie des nombres). Pour comprendre ce que signifie « premier », il peut être bon d’ailleurs de quitter un peu le domaine des nombres pour un exemple ou deux :

• En théorie des nœuds, on effectue des « multiplications » de nœuds. C’est tout simple, cela consiste à mettre ces deux nœuds bout à bout :

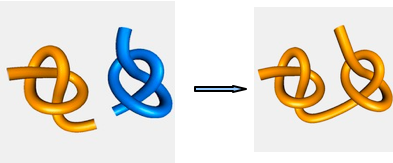
On peut ensuite les mélanger, changer la forme, cela ne change rien, il s’agit toujours du même nœud, sous un aspect différent. Un nœud résultat d’une multiplication est donc « composé ». À l’inverse, il existe des nœuds « premiers », qui ne sont pas décomposables en nœuds plus simples (vous pouvez en trouver des tableaux sur internet). On peut même faire une correspondance entre les nœuds et les nombres, les nœuds premiers correspondants naturellement aux nombres premiers, et leurs produits aux produits des nombres correspondants. Bien entendu, l’absence de nœud correspond au 1 : l’élément neutre, qui ne change pas le résultat d’une multiplication.

• En théorie des groupes également, on distingue les « groupes simples » que l’on ne peut pas obtenir en combinant d’autres groupes. Mais là, on est dans un monde bien différent des nombres et des nœuds.

Le fait qu’ils soient premiers se traduit par deux faits très importants : ils peuvent à eux seuls reconstruire tous les nombres, et ils ne font qu’une fois chaque nombre. Dit autrement, pour n’importe quel nombre, il existe une unique façon de l’écrire sous la forme d’un produit de nombres premiers. Cette propriété est la base de l’arithmétique, et montre à quel point il est important de bien comprendre les nombres premiers.

Le problème, c’est que chez les nombres premiers, tout est compliqué. Par exemple, depuis l’Antiquité, tout le monde se casse les dents sur les deux questions résolues pour les nombres triangulaires et carrés : trouver directement le n^ème, et trouver celui qui suit immédiatement un nombre donné. Et l’histoire de la théorie des nombres est grandement centrée sur ces deux problèmes…

Commençons par le commencement :

Dès l’Antiquité, des résultats et méthodes intéressants ont été trouvés. Le fameux crible d’Ératosthène, par exemple, qui permet en théorie de trouver tous les nombres premiers. L’idée est toute simple : on ne dispose pas de formule permettant de trouver tous les nombres premiers, ni même de trouver le nombre premier suivant un autre. Bref, en étant très négatif, la seule idée qui vient serait de prendre les nombres un par un et de les « tester » pour savoir s’ils sont ou non divisibles. En revanche, trouver des nombres qui ne sont pas premiers, c’est facile : il suffit de prendre par exemple tous les multiples d’un certain nombre. L’idée du crible est donc de barrer petit à petit tous les nombres qui ne sont pas premiers. Ceux qui restent le sont.

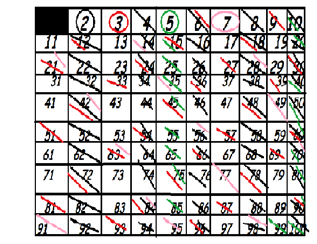
On commence donc par barrer un nombre sur deux à partir de 2 (en noir), puisque ce sont des multiples de 2. Puis on part du premier nombre qui n’est pas barré après de 2, 3 donc, et on barre un nombre sur 3 (en rouge), qui sont tous des multiples de 3. Évidemment, il arrive que l’on barre un nombre déjà barré, mais ce n’est pas grave. Et on recommence ainsi, indéfiniment. Au fur et à mesure, on obtient des nombres premiers. Mais ce qui est surprenant, c’est que ces nombres, qui sont issus comme on le voit ici de la superposition de « filtres » extrêmement réguliers, prévisibles, ne paraissent obéir à aucune règle, presque comme s’ils étaient disposés aléatoirement.

On conçoit bien grâce à cette méthode que plus on avance dans les nombres, moins on trouve de nombres premiers en proportion. Mais c’est à peu près tout ce qu’on arrive à dire, au moins dans un premier temps.

Il vient naturellement une question : à force de barrer des nombres, va-t-il en rester ? Dit autrement, y a-t-il un nombre fini ou infini de nombres premiers ? Euclide, au 3^è siècle avant JC, avait déjà répondu très clairement à cette question : supposons qu’il n’y ait qu’un nombre fini de nombres premiers. Pour ceux qui ont du mal quand il n’y a pas d’exemple numérique, mettons qu’on n’ait trouvé que 2, 3, 5 et pas d’autres. On se demande si on les a tous, si on parviendra à construire tous les nombres à partir de ceux là. Multiplions les tous ensembles, et ajoutons 1. On obtient 2 x 3 x 5 + 1. Ce nombre n’est pas divisible par 2, puisqu’il vaut deux fois quelque chose + 1. Il n’est pas non plus divisible par 3 ni par 5 pour la même raison. Dit autrement, pour ceux qui seraient sensibles aux nombres figurés, on ne pourra pas ranger ce nombre de cailloux sur 2 lignes, ni sur 3, ni sur 5. Bref, il ne peut pas être fabriqué à partir de ces trois nombres. Donc soit il est premier, soit il est composé à partir de nombres qui ne sont pas dans la liste dont nous disposions. Celle ci n’était donc pas complète ! Et évidemment, ce raisonnement peut être tenu avec une liste de n’importe quelle taille. Bref, quelle que soit la taille de la collection de nombres premiers donc vous disposez, ils ne suffiront jamais pour obtenir tous les nombres entiers, il y a donc bien une infinité de nombres premiers.

Ces résultats ne donnent encore qu’une image assez floue de l’emplacement des nombres premiers.

Les quelques tentatives pour trouver des formules donnant tous les nombres premiers n’ont pas été de grandes réussites : Fermat a tenté la formule 2^{2^n} + 1 (le ^ indique qu’on met encore à la puissance). Il avait trouvé qu’en remplaçant n par 1, 2, 3, et 4, on obtenait des nombres premiers. Pour n = 5, les calculs étaient un peu trop compliqués… manque de pot, pour 5 on obtient un nombre composé, et pour tous les autres nombres qui ont été testés depuis.

Autre tentative, plus réussie celle-ci, celle de Mersenne : Il proposa 2ⁿ – 1, en choisissant pour n un nombre premier. Cette formule est loin de fonctionner à tous les coups, et elle oublie beaucoup de nombres premiers. Mais elle en donne aussi beaucoup, et c’est même essentiellement grâce à elle que l’on connaît les plus grands nombres premiers actuels. (le plus grand connu aujourd’hui : 2^43,112,609– 1)

Des formules beaucoup plus tordues ont été trouvées au 20ème siècle, qui pour certaines donnent effectivement tous les nombres premiers, mais elles sont impraticables : soit elles demandent dans le calcul de passer par des nombres beaucoup trop grands, soit elles font appel à des constantes qui demandent pour être calculée… de connaître tous les nombres premiers ! Bref, on avance un peu, mais ce n’est pas la piste qui a pour l’instant fonctionné le mieux.

D’où d’autres angles d’attaques, des questions qui nous approchent tout de même des nombres premiers :

• À quelle vitesse se raréfient-ils ? Dit autrement, peut-on dire approximativement combien on trouve de nombres premiers entre 100 et 200 ? Entre un et deux millions ?

Les premières réponses à cette questions ne sont apparues qu’au 19^è siècle, et on n’a pas tout à fait fini.

• Quelle distance y a-t-il entre deux nombres premiers ? Cette question est posée depuis l’Antiquité, mais on ne sais toujours pas s’il y a un nombre fini ou infini de nombres premiers « jumeaux », ceux qui ne sont séparés que de 2, comme 17 et 19, par exemple.

Mais il y a tout de même des avancées. À force de calculer toujours plus de nombres premiers, les mathématiciens ont par exemple fini par trouver une sorte de régularité dans leur raréfaction : leur proportion suit une loi inverse du logarithme. Pour ceux qui ne connaissent pas, cela signifie qu’en gros, la proportion de nombres premiers parmi les nombres est inversement proportionnelle au nombre de chiffres qu’ont les nombres d’une certaine taille : 1/3 de moins autour de 1000 qu’autour de 1, donc, et ainsi de suite. Cette première approximation fut ensuite améliorée, avec une fonction proche du logarithme. Reste qu’évidemment, ce n’est qu’une approximation : si l’on suit ces fonctions, on monte en continu, alors qu’évidemment, les nombres premiers arrivent au coup par coup. Mais malgré tout, cette approximation est excellente : il a été démontré à la fin du 19^è siècle que plus on va loin dans les nombres, plus elle se rapproche de la véritable proportion.

Fait curieux : Gauss, qui proposa cette approximation, remarqua qu’elle était toujours légèrement au dessus de la réalité. Mais il se trompait. On a démontré qu’au bout d’un moment, les deux courbes se croisent. À quel moment ? Personne ne sait, mais très loin : au dernières nouvelles, c’est aux alentours de 1, × 10³¹⁶!

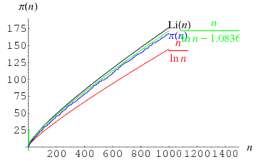
En rouge, vert et noir, des tentatives d’approximations du nombre de nombres premiers. En bleu, la véritable quantité de nombres premiers (remarquez les marches)

Si on va assez loin, la meilleure est largement la noire, celle proposée par Gauss, mais qui est un peu trop haute… pendant un certain temps !

Une autre piste… La fonction zêta de Riemann

Bon, impossible de parler des nombres premiers sans parler de Bernhard Riemann. Tout cela risque de devenir un peu technique, mais on peut essayer de suivre les grandes lignes sans rentrer dans les détails. La fonction zêta (ζ) est définie ainsi : ζ(s) = 1/2^s + 1/3^s + 1/4^s + …

Il n’est certainement pas évident pour tout le monde d’envisager ce que signifie une somme infinie, une puissance autre qu’entière, et pourtant les mathématiciens ont réussi à donner un sens à ce genre d’expressions.

Premier coup de génie : faire le lien entre cette fonction et les nombres premiers. L’idée est d’Euler, elle est d’une simplicité déconcertante et en même temps très forte : si on multiplie tous les nombres premiers et leurs puissances entre eux, on reconstitue tous les nombres entiers. Pour le dire de façon je l’espère un peu plus simple : prenez le produit (1 + 2 + 2² + 2³ + …) X (1 + 3 + 3² + 3³ + …) X (1 + 5 + 5² + 5³ + …) x … dans lequel dans chaque parenthèse se trouve la somme de toutes les puissances d’un nombre premier, et en imaginant qu’on les prend tous. Imaginez que l’on développe ce produit. On retrouve alors 1 en prenant le 1 de chaque parenthèse, le 2 en « choisissant » le 2 dans la première parenthèse et le 1 dans toutes les autres, le 6 en choisissant le 2 dans la première, le 3 dans la deuxième et le 1 dans toutes les autres, et ainsi de suites. Tous les nombres entiers seront bien reconstitués, chacun en exactement un exemplaire !

(détails pour les plus enthousiastes seulement…

La formule d’Euler est celle-ci : 1/(1-1/2^s) X 1/(1-1/3^s) X 1/(1-1/5^s) X 1/(1-1/7^s)… Prenons un seul de ces termes, le premier par exemple : 1/(1-1/2^s). Il se trouve que ceci est égal à 1 + 1/2^s + 1/2^2s + 1/2^3s + … Cette égalité est classique, elle est bien connue de toute personne ayant fait au moins une année d’étude avec des maths. En résumé donc, dans chacun des termes de la multiplication, on trouve toutes les puissances d’un inverse de nombre premier (à la puissance s), et 1. Réécrivons le : (1 + ½^s + 1/2^2s + 1/2^3s + …) X (1 + 1/3^s + 1/3^2s + 1/3^3s + …) X (1 + 1/5^s + 1/5^2s + 1/5^3s + …) X …

On trouve donc, si on prend ce produit dans son ensemble, tous les résultats envisageables en multipliant des nombres premiers et leurs puissances entre eux, c’est à dire exactement tous les nombres entiers.)

Bref, cette fonction, étudiée à l’origine pour autre chose, se trouve très fortement liée aux nombres premiers. Et là, attention ça se corse encore : Riemann parvient à donner un sens à cette expression en donnant à s n’importe quelle valeur… complexe ! Impossible d’expliquer rapidement à ceux qui n’ont jamais rencontré les nombres complexes ce qu’ils sont. Disons pour résumer que cette fameuse fonction ζ peut être appliquée sur tous les points d’un plan : en chaque point, une valeur peut être calculée. (une petite image pour souffler : les couleurs dépendent des valeurs prises par la fonction.)

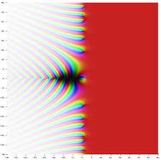
En certains endroits, cette valeur est nulle (les petites zones sombres). C’est le cas pour tous les points qui se trouvent sur l’axe horizontal en coordonnées -2, -4, -6, …, ce pour quoi on dispose d’une explication simple. Mais il y a d’autres endroits sur le plan où cette fonction prend la valeur 0. Dans un tout petit texte de 1859, Riemann dit en substance : « J’en ai calculé quelques un, ils ont l’air d’être tous alignés sur une même droite verticale. Mais je n’ai pas trouvé de démonstration, et ça ne m’intéresse pas directement pour ce que j’ai à dire ici ». Le truc, c’est que ces fameux points où la fonction s’annule vont s’avérer essentiels pour mieux comprendre comment les nombres premiers se répartissent. Et cette petite remarque de Riemann va devenir de plus en plus importante, au point qu’en 1900, à la fameuse conférence donnée par David Hilbert pendant laquelle il a donné une liste de 23 problèmes pour « guider » les mathématiciens du 20ème siècle, l’hypothèse de Riemann est le 8^ème de la liste. Aujourd’hui, c’est l’un des rares à n’avoir pas été résolu, et le seul à figurer à nouveau sur la liste des 7 problèmes du millénaire mis à prix à un million de dollars en 2000 par l’Institut Clay.

Pourtant, les résultats qui « cernent » cette conjecture s’accumulent :

• On sait que les « zéros » se trouvent tous « à proximité » de cette droite
• On sait qu’il y en a une infinité dessus (on sait même qu’il y en a au moins 2/5 ème)
• On en a calculé plus de 10 000 milliards, et ils sont effectivement tous sur cette droite

Bref, aujourd’hui tout le monde est à peu près convaincu que cette conjecture est juste, mais il n’y a toujours pas de démonstration. L’attente se fait d’autant plus sentir que de plus en plus, plusieurs théories se sont développées en supposant que la conjecture est juste !

Pour finir, un petit inventaire à la Prévert de questions qui restent posées :

• La conjecture des nombres premiers jumeaux : ce sont les nombres premiers qui ne sont séparés que de 2 (c’est à dire les plus proches possibles quand on a passé 2). Y en a-t-il un nombre fini ou infini ?
• La conjecture de Goldbach : Est il toujours possible d’écrire un nombre pair sous la forme d’une somme de deux nombres premiers ?
• En 1972, grosse surprise : Montgomery, un mathématicien et Dyson, un physicien discutent de leurs sujets de recherche respectifs, et réalisent que la répartition des zéros de la fonction ζ sur la fameuse droite obéit à la même loi qu’un outil mathématique a priori sans aucun rapport qui sert à modéliser les différents niveaux d’énergie dans les atomes ! Qui pourra expliquer ça ?
• Savoir dire rapidement à la vue d’un nombre s’il est premier ou pas. On dispose de tests plus rapides que celui qui consiste à essayer « bêtement » tous les diviseurs possibles un par un, mais pas forcément aussi fiables. Il existe ainsi des nombres « pseudo-premiers » qui passent certains tests, et pourraient faire croire un instant qu’ils sont premiers…
• Savoir retrouver rapidement les facteurs premiers d’un nombre, quand ceux-ci sont grands. Cela dit, pour l’instant cette incapacité est plutôt une bonne nouvelle : c’est comme ça qu’on code nos messages sur internet…

Sachant que l’hypothèse de Riemann arrive très nettement en tête, car elle ouvrirait sans doute très largement le panorama… Hilbert disait d’ailleurs : « Si je devais me réveiller après avoir dormi pendant mille ans, ma première question serait : L’hypothèse de Riemann a-t-elle été prouvée ? »

Et juste pour finir sur une note optimiste, un théorème récent (de Green et Tao) que je trouve très joli : on peut trouver des suites aussi longues qu’on le souhaite de nombres premiers espacés régulièrement. (mais on ne dit pas de combien, ni comment les trouver, faut pas rêver!)